1. 资源

百科：

网址：

2. MT策略

MT策略即动量交易策略（Momentum Trading Strategy）。在经典力学里，动量指的是物体的质量和速度的乘积。牛顿当初在创造动量这个概念时，意图捕捉的是“运动的量”这个概念。所以我们可以理解为物体必须有运动才会有动量。背后的直觉是：当物体有运动，就会有速度；速度加上物体本身的质量，就决定了动量。速度和质量一方面描述了物体的运动状态，另一方面也刻画出其保持已有运动状态的趋势，即惯性大小。

（1）动量效应产生的原因

对于证券市场上动量效应的产生原因，传统金融学与行为金融学有截然不同的看法。传统金融学在保留期望效用与理性人假设的前提下，试图引入更多的风险因子，以便产生新的风险溢酬来捕捉动量效应产生的超额收益。一般而言，这些尝试并没有获得广泛的认可，同时也存在是否过度拟合的疑虑。与传统金融理论相悖，行为金融学则认为投资人在复杂的市场环境中无法完美地预期与判断，故有“非理性”的行为与随之而来的定价偏差;同时，套利者受限于市场机制与风险承担能力，也不一定能及时纠正偏差的价格。不过，真正的原因何在，说法却不一而足。较为人所熟知的有“反应不足”、“正反馈模式”和“过度反应”等见解。

针对第一种说法“反应不足”举例来说，当上市公司出现利好信息时，其证券价格会随之上涨，但由于投资者没有及时地接收、消化这一信息，价格对此信息的反应无法一步到位。如百度公司发布其年中财报，财报显示百度公司运营很好。投资者A可能是在财报发布当下即购买百度股票，投资者B在五天后才看到这个财报，其又观望了一天，然后再去购买百度股票。对于百度的股价来说，这个利好信息本身应导致百度股价上涨;市场上A类的投资者，会使百度股价在财报发布的当下做出反应;但由于市场上还有很多信息反应不足的B类投资者，百度股价上涨会持续一段时间，因而产生百度股价的动量效应。

另一种说法“正反馈模式”，借由羊群效应来说明动量产生的原因。大多数投资人有从众心理，认知或判断倾向于公众舆论或行为，证券市场即有“赢者恒赢，输者恒输”的现象。

第三种说法“过度反应”，是指投资人对私有信息的预测性，自身的投资判断能力等高估而产生的过度反应。更甚者，短期的趋势变化“不出所料”这个心理、行为现象会被进一步强化。

上述三种行为金融的理论除了解释的角度有所差异外，其预测的现象也不尽然相同。“反应不足”预测动量效应只存在于短期，会随着时间的延长而逐渐消失。“正反馈模式”与“过度反应”则认为动量为短期偏离基本价值的泡沫，当泡沫随着时间拉长而有朝一日破裂时，股价便会反转。

（2）价格动量的计算公式

【1】作差法求动量值

作差法，即今天的价格减去一段时间间隔（m期）以前的价格，用公式表示 t 时期的二期动量Momentum*为：

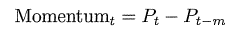
其中，P_t为股票 t 时期的价格，m 表示时间间隔，P_{t-m}为股票在 t-m 期的价格。

• 计算万科股票收盘价的 5 期动量值

--------------------------------------导入相关包-----------------------------------
import pandas as pd
import matplotlib.pyplot as plt

--------------------------------获取万科股票日度数据---------------------------------
Vanke = pd.read_csv('wanke_data.csv')

Vanke.index=Vanke.iloc[:,1]
Vanke.index=pd.to_datetime(Vanke.index, format='%Y-%m-%d')
Vanke=Vanke.iloc[:,2:]

# 提取收盘价
Close = Vanke.Close

# 求滞后5期的收盘价变量
lag5Close = Close.shift(5)

# 求5日动量
momentum5 = Close-lag5Close

--------------------------------绘制收盘价和5日动量曲线图---------------------------
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(12,6))

plt.subplot(211)
plt.plot(Close,'b*')

plt.xlabel('date')
plt.ylabel('Close')
plt.title('万科股价5日动量图')

plt.show()

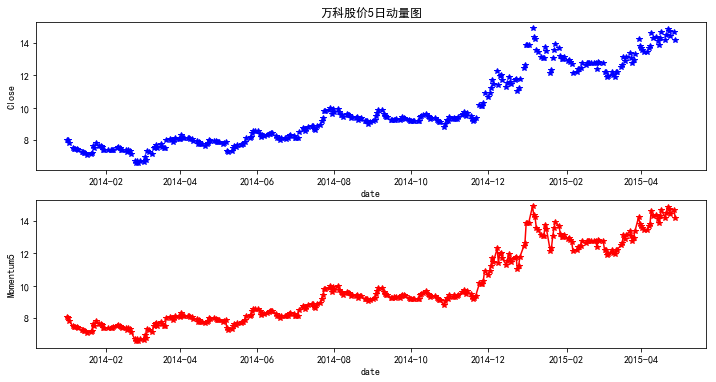
【2】作除法求动量值

动量的另一种计算方式是做除法，即 t 期的价格减去其 m 期以前的价格 P_{t-m}，再除以P_{t-m}。做除法求出的动量值衡量的是价格变化的比率，用公式表示 t 时期的 ROC（Rate of Change）为：

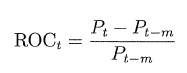
其中，ROC_t 表示股票 t 时期的 m 期动量值（价格变化率），P_t 表示股票 t 时期的价格，m 表示时间间隔，P_{t-m}表示股票在 t-m 期的价格。

• 计算万科股票收盘价的 5 期动量值

# 作除法，求万科股票的5日动量值
Momen5 = Close/lag5Close - 1
Momen5 = Momen5.dropna()

（3）编写动量函数 momentum()

动量值一般采用作差法求得，为了计算动量值方便，此处编写一个简单的动量函数momentum()，该函数有价格 price 和期数 period 两个参数，函数定义如下:

def momentum(price,periond):
    lagPrice=price.shift(periond)
    momen=price-lagPrice
    momen= momen.dropna()
    return(momen)
    
-------------------------------调用函数求动量值------------------------------------
momentum5 = momentum(Close,5)
momentum5.head()

（4）万科股票2015年走势及35日动量线

-----------------------万科股票2015年走势及35日动量线-------------------------------
# 计算35动量值
momen35 = momentum(Close,35)

import candle            # K线图策略下载candle.py模块
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12,12))

Vanke15 = Vanke['2015']

candle.candleLinePlots(Vanke15,candleTitle='万科股票2015年日K线图',
                       splitFigures=True,Data=momen35['2015'],title='35日动量',
                       ylabel='35日动量')

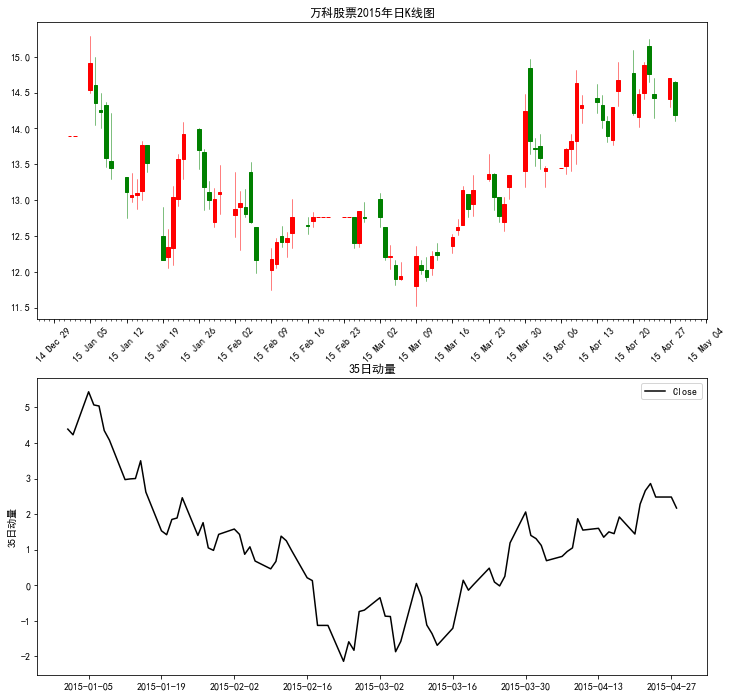
（5）动量交易策略的一般思路

运用动量指标制定交易策略，常用的交易策略可以总结为下面的四个步骤。

• 获取股票价格(一般为收盘价)数据;

• 确定时间跨度和动量表达式，计算股票的动量值;

• 根据动量指标制定交易策略;在动量指标运用上，最直觉的交易策略是动量大于0，说明股票可能还具备上涨的能量，释放出买入的信号;当股票的动量值小于0，说明股票可能有下跌的能量，释放出卖出信号。简而言之，若动量大于0，则买入股票;若动量小于0，则卖出股票。

• 交易策略的回测与评价。

【1】运用动量指标交易万科股票

结合动量指标的交易思想，用Python编写代码来捕捉市场中的可能买卖点。从动量的计算公式可以看出，动量值的大小与时间跨度。有很大的关系，在时间跨度。的设定上，见仁见智，没有统一标准。在本次的动量指标计算中，将时间跨度设定为35日，根据35日动量的取值情况来捕捉买卖点。

• 当35日动量为正值时，市场可能还存在上升的能量，我们推断第2期可以进行买入操作;

• 当35日动量为负值时，我们预期未来价格可能要下跌，第2期可以进行卖出操作。

还请注意，在投资实战中，投资者会综合多种指标和形态来确定买入点和卖出点。为了着重体现动量指标的交易思想，这里假定买卖操作的确定只依据动量这一个指标。

• 首先提取出万科股票的收盘价数据，计算35日动量值。

# 提取万科股票收盘价格数据，计算35日动量值
Close = Vanke.Close
momen35 = momentum(Close,35)

• 结合35日动量值的取值情况来判断买卖点，35日动量释放的买卖点信号用signal表示。

#当35日动量值为负值时，signal取值为一1，表示卖出;
#当35日动量值为非负值时，signal取值为1，表示买入;
signal=[]
for i in momen35:
    if i>0:
        signal.append(1)
    else:
        signal.append(-1)
      
signal = pd.Series(signal,index=momen35.index)

• 根据买卖点制定买入和卖出交易，并计算收益率。

tradeSig = signal.shift(1)
ret = Close/Close.shift(1) - 1

Mom35Ret = ret*(signal.shift(1))

• 35日动量指标交易策略评价。

35日动量指标交易策略确捕捉到买卖点信号以后，我们来计算一下该35日动量指标买卖点预测的准确率。当出现买入信号时，signal取值为1，当我们预计的价格上涨这件事发生了(也就是预测准确，收益率大于0)，则signal与ret的乘积大于0。当出现卖出信号时，signal取值为一1，且预测准确时，收益率小于0 9 signal(取值为一1)与re七(负值)的乘积也是大于0。当35日动量值交易的收益率大于0时，则说明买卖点预测正确。

-----------------------绘制出万科股票收益率与动量指标交易策略收益率的时序图--------------------------
-------------------------------------------------------------------------------------------------
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,8))

plt.subplot(2,1,1)
plt.plot(real_ret,'b')
plt.ylabel('return')
plt.title('万科收益率时序图')

plt.subplot(2,1,2)
plt.plot(Mom35Ret,'r')
plt.ylabel('Mom35Ret')
plt.title('万科动量交易收益率时序图')

plt.show()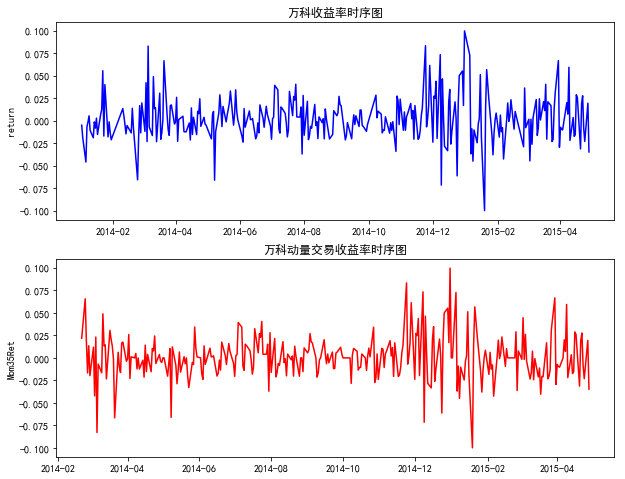

# 计算指标交易获胜率
win = Mom35Ret[Mom35Ret>0]
winrate = len(win)/len(Mom35Ret)
loss = -Mom35Ret[Mom35Ret<0]

-------------------------------绘制出万科股票盈利与损失收益率的直方图------------------------------
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,8))

plt.subplot(2,1,1)
win.hist()
plt.title("盈利直方图")

plt.subplot(2,1,2)
loss.hist()
plt.title("损失直方图")

plt.show()

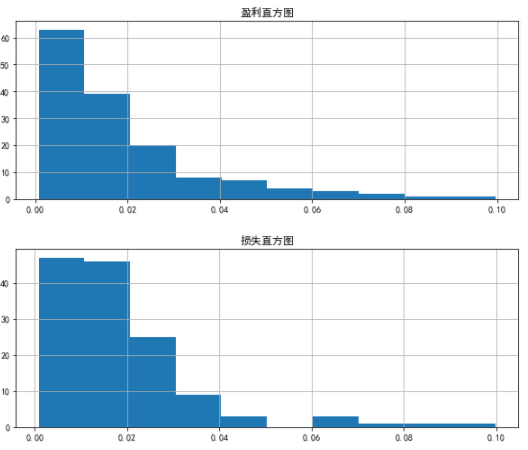
• 计算两种收益率的平均值与分位数值

# 计算两种收益率的平均值与分位数值
performance=pd.DataFrame({"win":win.describe(),"loss":loss.describe()})
performance

从两种收益率的分位数分布情况可以看出，尽管万科股票35日动量指标交易策略预测准确率高于0.5，但是动量指标预测错误时损失的收益率整体比预测准确时盈利的收益率大。

3. 作业

【1】（600000.csv）获取“浦发银行”（股票代码为“600000"）2014年的日度交易数据。

  (a) 请用两种不同的方法分别计算6日动量值、30日动量值和90日动量值；

  (b) 用Python编写动量指标交易策略，交易策略如下:

• 若当期动量值大于0，市场的上涨趋势较大，signal为1，第2期买入股票(信号出现时为第1期)；

• 若动量值小于。时，市场的下跌趋势较明显，signal为一1，卖出股票；分别用G日动量值、30日动量值和90日动量值制定上述交易策略，计算并比较这3个动量值买卖点预测准确率。

4. 附件