1.5  建模示例之三  椅子能在不平的地面上放稳吗

背景和问题：

把椅子往不平的地面上一放，通常只有三只脚着地，放不稳，然而只需挪动几次，就可以使四只脚同时着地，放稳了。这个看来似乎与数学无关的现象能用数学语言给以表述，并用数学工具来证实吗？

问题分析：

通常 ~三只脚着地，放稳 ~四只脚着地

模型假设：

• 四条腿一样长，椅脚与地面点接触，四脚连线呈正方形;

• 地面高度连续变化，可视为数学上的连续曲面;

• 地面相对平坦，使椅子在任意位置至少三只脚同时着地.

模型构成：

用数学语言把椅子位置和四只脚着地的关系表示出来.

• 椅子位置：利用正方形(椅脚连线)的对称性. 用q(对角线与x轴的夹角)表示椅子位置.

• 四只脚着地：椅脚与地面距离为零；距离是q 的函数.

  四个距离(四只脚) 正方形对称性 两个距离

      A,C 两脚与地面距离之和~ f(q)

      B,D 两脚与地面距离之和~ g(q)

  正方形ABCD绕O点旋转

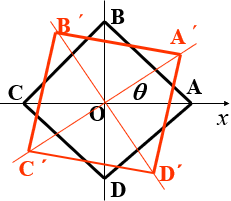
• 用数学语言把椅子位置和四只脚着地的关系表示出来.

• 地面为连续曲面，f(q) , g(q)是连续函数

• 椅子在任意位置至少三只脚着地，对任意q, f(q), g(q)至少一个为0

• 数学问题：已知：f(q) , g(q)是连续函数;  对任意q，f(q) • g(q)=0 ; 且 g(0)=0，f(0) > 0. 证明：存在q0，使f(q0) = g(q0) = 0.

模型求解：

  给出一种简单、粗糙的证明方法：

     1）将椅子旋转90o，对角线AC和BD互换.

   由g(0)=0，f(0) > 0，知 f(p/2)=0,  g(p/2)>0.

     2）令 h(q)= f(q)–g(q), 则 h(0)>0和h(p/2)<0.

     3）由f, g 的连续性知 h为连续函数,  据连续函数的基本性质, 必存在q0 ( 0< q0 < p/2) , 使h(q0)=0, 即f(q0) = g(q0) .

      4）因为 f(q) • g(q)=0, 所以 f(q0) = g(q0) = 0.

评注和思考：

• 建模的关键：用q表示椅子的位置，用f(q), g(q)表示椅脚与地面的距离

• 假设条件中哪些是本质的,哪些是非本质的? 

  考察四脚连线呈长方形的椅子 (习题4).

• 证明过程的粗糙之处：

  椅子的旋转轴在哪里，它在旋转过程中怎样变化？