1.6  数学建模的基本方法与步骤

• 基本方法：机理分析与测试分析

• 机理分析：根据对客观事物特性的认识，找出反映内部机理的数量规律

• 测试分析：将对象看作“黑箱”,通过对量测数据的统计分析，找出与数据拟合最好的模型。

• 在建模中的应用：用机理分析建立模型结构,用测试分析确定模型参数。能将道理讲道理，讲不清道理讲数据。

• 建模步骤：模型准备，模型假设，模型构成，模型求解，模型分析，模型检验，模型应用。

• 模型准备：了解实际背景，明确建模目的，搜索相关信息，把握对象特征，形成一个较为“清晰”的问题。

• 模型假设：分析影响因素，分析设置变量，假设变量之间的关系，要在合理（保真）和简化（可行）之间折中，是数学建模艺术之所在。

• 模型构成：用数学语言，符号描述问题（特有规律的数学表示）。尽量采用简单的数学工具。

• 模型求解：数学方法，软件和计算机求解析解，近似解或数值解。

• 模型分析：对结果进行误差分析，统计分析，敏感性分析，对算法和数据进行稳定性分析，对模型进行稳健性分析。

• 模型检验：与实际现象、数据比较，检验模型的合理性、适用性。

• 模型应用：把数学模型的结果翻译回原问题，解决实际问题。

• 建模的全过程（四个环节，两个世界，双向翻译）

  掌握框图：

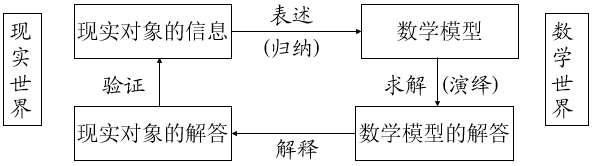
• 四个环节：

 表述（Formulation)-根据建模目的和信息将实际问题“翻译”成数学问题

 求解（Solution)-选择适当的数学方法求得数学模型的解答.

 解释（Interpretation)-将数学语言表述的解答“翻译”回实际对象.

 验证（Verification)-用现实对象的信息检验得到的解答.