2.3  实物交换

背景和问题：

甲有物品X, 乙有物品Y, 双方为满足更高的需要，商定相互交换一部分. 研究实物交换方案.

分析与建模：

甲的无差别曲线

• 如果甲占有(x1,y1)与占有(x2,y2)具有同样的满意程度, 即p1,p2对甲是无差别的. 将所有与p1,p2无差别的点连接起来, 得到一条无差别曲线MN.

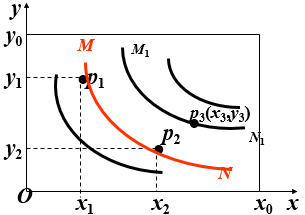
• 线上各点的满意度相同, 线的形状反映对X,Y的偏爱程度.

• 比MN各点满意度更高的点如p3，在另一条无差别曲线M1N1上, 于是形成一族无差别曲线（无数条）.

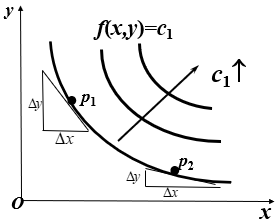
• 甲的无差别曲线族记作f(x,y)=c1，c1~满意度（f ~等满意度曲线）

无差别曲线族的性质：

• 单调减(x增加, y减小)；下凸(凸向原点)；互不相交

• 乙的无差别曲线族g(x,y)=c2具有相同性质（形状可以不同）

双方的交换路径：

• 甲的无差别曲线族 f=c1

• 乙的无差别曲线族 g=c2 (坐标系x'O'y', 且反向）

• 两族曲线切点连线记作AB

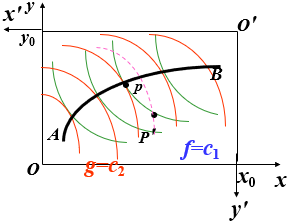
• 双方满意的交换方案必在AB（交换路径）上!

  因为在AB外的任一点p', (双方)满意度低于AB上的点p.

交换方案的进一步确定：

• 交换方案 ~交换后甲的占有量(x,y)

      0£x£x0, 0£y£y0矩形内任一点  交换路径AB

       AB与CD的交点p （等价交换原则）

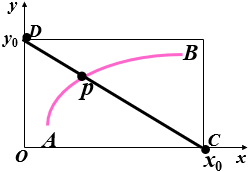
• 设X单价a, Y单价b, 则等价交换下ax+by=s (s=ax0=by0)