2.4  汽车刹车距离与道路通行能力

背景和问题：

• 现代城市生活中交通拥堵是普遍存在的现象，提高道路通行能力，已经成为城市交通工程面临的重要课题之一。

• 车辆速度越高、密度越大，道路通行能力越大；车速高，刹车距离变大，车辆密度将受到制约。需要对影响通行能力的因素进行综合分析。

• 介绍交通流的基本参数及它们之间的关系；讨论汽车刹车距离与道路通行能力两个模型。

（1）交通流的基本参数及其特性

    流量q，流速v，密度k，三个参数之间的基本关系 q=kv

速度v和流量k的关系模型：

• 线性模型 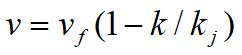~适合车流密度适中的情况

    vf ~畅行车速(k=0时), kj ~阻塞密度(v=0时)

• 对数模型 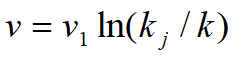          ~车流密度较大时适用

      v1~k=kj/e时的车速(理论上), 由观测数据确定.

• 指数模型 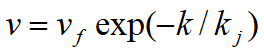~车流密度较小时适用 

交通流的基本参数及其特性:

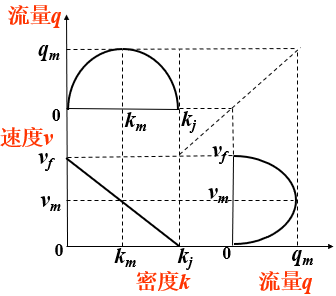
        km=kj /2 ~最大流量时的密度；vm=vf /2 ~最大流量时的速度 

（2）汽车刹车距离模型

• 刹车距离——从司机决定刹车到车完全停止行驶的距离.

• 车速越快刹车距离越长，二者是线性关系吗？

测试数据：

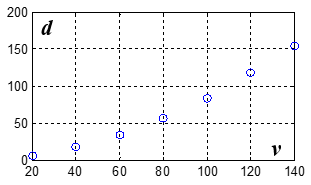
•  d 与v不是线性关系！需对刹车过程作机理分析，建立d 与v的数学模型.

问题分析：

• 刹车距离——反应距离、制动距离

• 反应距离——司机决定刹车到制动器开始起作用。

• 制动距离——制动器开始起作用到汽车完全停止。

• 反应距离由反应时间和速度决定，而反应时间司机状况、制动系统的灵活性（可看作常数）来决定。

• 制动距离由制动器作用力、车重、车速、道路、气候…（看作常数）决定。最大制动力与车质量成正比,使汽车作匀减速运动。

模型假设：

 1.刹车距离d 为反应距离d1与制动离d2之和.

 2.反应距离d1与车速v 成正比, 比例系数为反应时间.

 3.刹车时使用最大制动力F ：

• F作的功等于汽车动能的改变；F与车的质量m 成正比.

模型建立：d = d1 +d2，d1=c1v

• 制动距离为d2时，制动力F作的功为Fd2

• 车速从v变成0，动能的变化为

• 调查交通工程学的相关资料：司机反应时间c1约为0.7~1s，系数c2约为0.01( )

（3）道路通行能力模型

• 道路通行能力——单位时间内通过某断面的最大车辆数.

• 通行能力表示道路的容量，交通流量表示道路的负荷.

• 饱和度——流量与通行能力的比值, 表示道路的负荷程度.

• 通行能力——在安全条件下，当具有标准长度和技术指标的车辆，以前后两车最小车头间隔连续行驶时，单位时间内通过道路某断面的最大车辆数N (辆/h).

• v~车速(km/h)，D~最小车头间隔(m)，则 N=1000v/D

• 最小车头间隔D主要由刹车距离d决定：  D=d+d0，，

  d0~车身标准长度与两车间安全距离之和，取固定值。    

• 车速v一定时，道路通行能力N与c1，c2，d0（道路、车辆、司机等状况）有关。

• 在道路、车辆、司机等状况不变时，车速v多大可使通行能力N达到最大。 

• 利用初等方法求得，当时，最大通行能力为

• 当d0，c1，c2变大时最大通行能力Nm减小。