3  简单的优化模型

• 现实世界中普遍存在着优化问题.  如......

• 静态优化问题指最优解是数(不是函数).

• 建立静态优化模型的关键之一是根据建模目的确定恰当的目标函数.

• 求解静态优化模型一般用微分法.

3.1  存储模型

背景与问题：

• 配件厂为装配线生产若干种产品，轮换产品时因更换设备要付生产准备费，产量大于需求时要付贮存费. 该厂生产能力非常大，即所需数量可在很短时间内产出.

• 已知某产品日需求量100件，生产准备费5000元，贮存费每日每件1元. 试安排该产品的生产计划，即多少天生产一次（生产周期），每次产量多少，使总费用最小.

• 要求：不只是回答问题，而且要建立生产周期、产量与需求量、准备费、贮存费之间的关系.

问题分析与思考：

• 周期短，产量小 → 贮存费少，准备费多

• 周期长，产量大 → 准备费少，贮存费多

• 存在最佳的周期和产量，使总费用（二者之和）最小.

• 这是一个优化问题，关键在建立目标函数.

• 目标函数——每天总费用的平均值.

模型假设：

  1.产品每天的需求量为常数r；

  2.每次生产准备费为c1, 每天每件产品贮存费为c2；

  3.T天生产一次（周期）, 每次生产Q件，当贮存量为零时，Q件产品立即到来（生产时间不计）；

  4.为方便起见，时间和产量都作为连续量处理.

建模目的：

• 设r,c1,c2已知，求T,Q使每天总费用的平均值最小.

模型建立：离散问题连续化

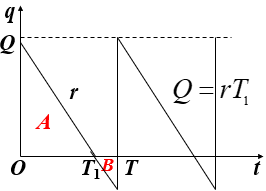
• 图示：

• 贮存量表示为时间的函数q(t)

  t=0生产Q件，q(0)=Q,q(t)以需求速率r递减，q(T)=0.

  

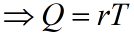
• 一周期贮存费为

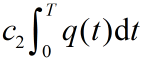
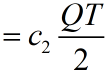
• 一周期总费用

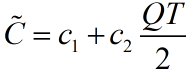
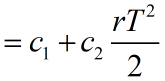
不容许缺货的存储模型：准备费+贮存费

• 每天总费用平均值（目标函数）

模型求解：

• 求T 使

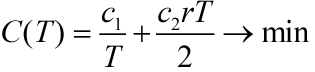
• 令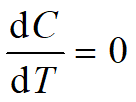，求解得到， ,

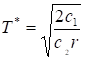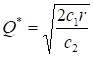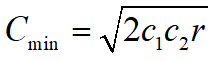
模型解释：

• 定性分析：，，

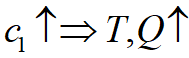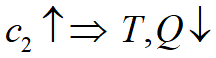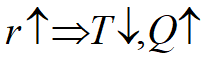
• 敏感性分析：参数c1, c2, r的微小变化对T, Q的影响

     T对c1的(相对)敏感度： 

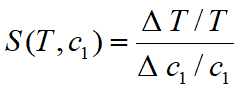
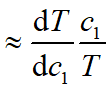
    ，S(T,c2) = –1/2, S(T,r) = –1/2.

     c1增加1%, T增加0.5%，c2或r增加1%, T减少0.5%

模型应用：

• 回答原问题：c1=5000, c2=1，r=100

  T=10(天), Q=1000(件), C=1000(元)

• 思考: 为什么与前面计算的C=950元有差别?

• 用于订货供应情况:

  每天需求量r，每次订货费c1, 每天每件贮存费c2, T天订货一次(周期), 每次订货Q件，当贮存量降到零时，Q件立即到货.

• 经济订货批量公式（EOQ公式）Economic Order Quantity

允许缺货的存贮模型：

• 准备费+贮存费+缺货费，订货周期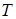，订货量的二元函数，图示：

  开始缺货时间，

• 总费用

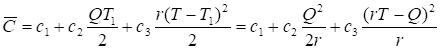
• 平均每天的费用

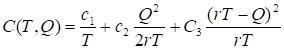
  求T ,Q，使 

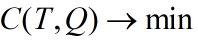
• 求导得到：

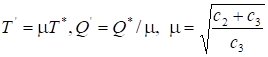
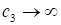• 相当于允许缺货.