3.3  森林救火

背景与问题：

• 森林失火后，要确定派出消防队员的数量.

• 队员多，森林损失小，救援费用大；

• 队员少，森林损失大，救援费用小.

• 综合考虑损失费和救援费，确定队员数量.

问题分析：

• 记队员人数x, 失火时刻 t=0, 开始救火时刻 t1, 灭火时刻 t2, 时刻 t 森林烧毁面积 B(t).

• 损失费 f1(x)是 x 的减函数, 由烧毁面积 B(t2)决定.

• 救援费 f2(x)是x的增函数, 由队员人数和救火时间决定.

• 存在恰当的x，使f1(x), f2(x)之和最小.

• 建立救火模型并求解，并对模型假设进行分析和推广.

建模和求解：

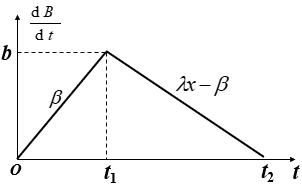
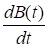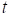• 画图表示对变化图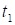，为开始救火时刻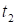，为火灭时刻，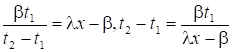

  
  

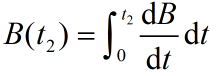
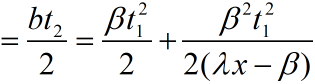
• 损失费和救援费：

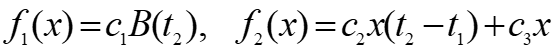
• 目标函数——总费用：

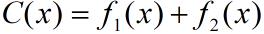
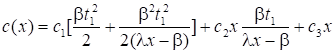
• 求解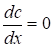，得到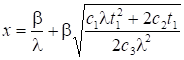

  
  

结果解释：

• b /l是火势不继续蔓延的最少队员数

• c1~烧毁单位面积损失费, c2~每个队员单位时间灭火费, c3~每个队员一次性费用,  t1~开始救火时刻, b~火势蔓延速度,  l~每个队员平均灭火速度.  c1,t1,b  ↑ ® x­ ↑；c3,l ↑ ® x↓  

模型应用：

• c1,c2,c3已知, t1可估计, b ,l可设置一系列数值

• 由模型决定队员数量 x

课后扩展阅读：