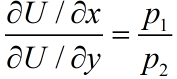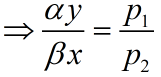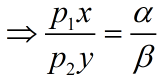3.3  不买贵的只买对的

背景和问题：

• 消费者在琳琅满目的市场里选购商品，如何分配手里一定数量的钱，选择购买若干种需要的商品？——“不买贵的，只买对的”！

• 根据经济学的一条最优化原理——“消费者追求最大效用” ，用数学建模的方法帮助消费者决定他的选择.——效用函数

• 先假定只有甲乙两种商品供消费者购买，建立的模型可以推广到任意多种商品的情况.

建模和求解：

• 效用函数(utility function)：

• 定量描述吃下面包、缓解饥饿、满足生理和心理需求程度的变化.

  U(x)吃x片面包获得的满足程度(面包产生的效用).

  △U(x)=U(x)-U(x-1) 每多吃1片面包所产生效用的增量.

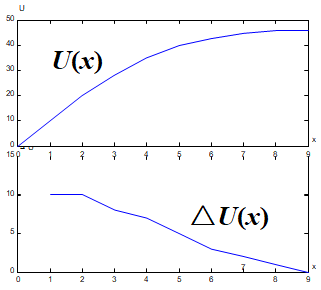
• U(x)递增, 增长渐慢, 曲线上凸. 

• △U(x)≥0,递减, 曲线下降.

• 效用人们在商品或服务消费中获得的生理、心理上的满足程度.

  效用函数U(x) 数量为x的某种商品产生的效用.

• 边际效用——dU(x)/dx x增加1个单位U(x)的增量.

• 典型的效用函数：

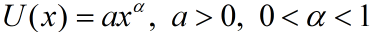
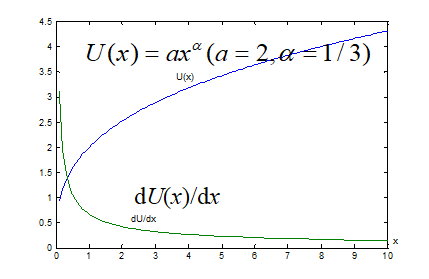
• U(x)>0,递增渐慢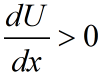；,递减； 

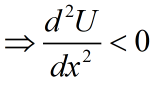
• “边际效用递减” 经济学中普遍、重要的法则.现实生活中的诸多表现...

• 效用函数和边际效用特性的数学表述：效用递增；边际效用递减

• 无差别曲线：U(x,y)两个变量x, y的效用函数

  x片面包和y根香肠的组合

  几种组合的效用函数相等 U(x,y)=u1 (u1常数)

• 无差别曲线效用函数的几何表示.——等效用线

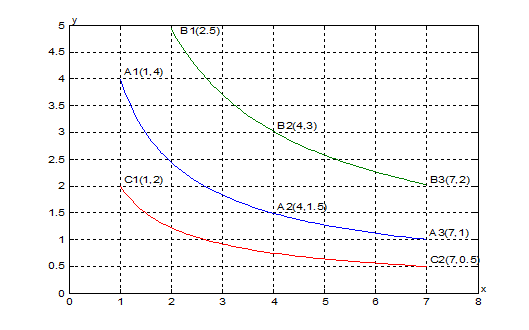
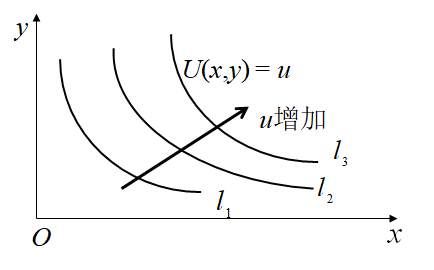
  效用函数值u增加无差别曲线上移

• 典型的效用函数：
  

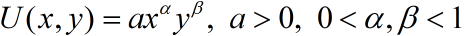
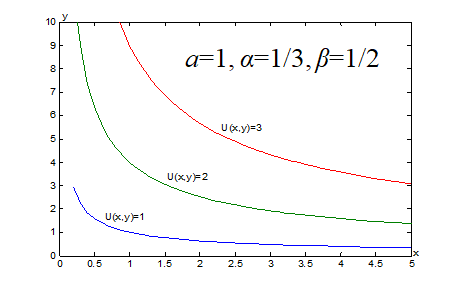
• 无差别曲线的特性：几何直观：下降、下凸、互不相交

  “下降”的数学解释；“下降”的经济学解释

  “下凸”的经济学解释

  “互不相交”的解释

效用最大化模型：

• 问题：已知甲乙两种可替代商品的效用函数, 用一定数额的钱购买多少甲、多少乙？

• 由效用函数最大确定购买数量效用最大化原理

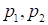
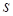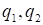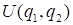• x, y购买甲乙商品数量，U(x, y)效用函数，甲乙商品的单价,s准备付出的钱，试分配,确定购买甲乙数量,使最大.

• 效用最大化模型具有等式约束的最大值问题

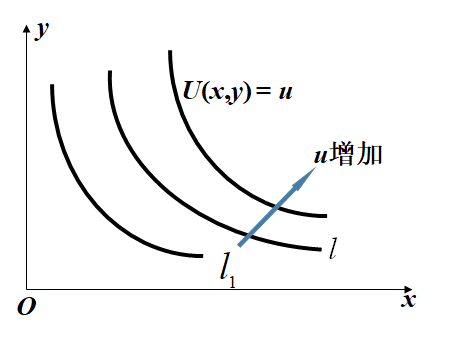
模型求解——几何分析：

• U(x,y)=u 下降、下凸、互不相交的无差别曲线.

  AB必与一条无差别曲线l，相切于Q点——消费点

  消费点Q (x, y)的U(x,y)最大

模型求解——二元函数条件极值

• 求解约束最大值问题的乘子法步骤：

 （1）构造函数：

 （2）求的无约束极值问题.

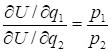
• 均衡消费条件边际效用之比等于价格之比.

• 效用函数与无差别曲线的关系：效用函数的等值性就是无差别曲线，即由隐式方程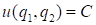确定函数曲线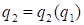为无差别曲线.

• 几何分析与条件极值结果的一致.

典型例子：

• 购买两种商品费用之比等于参数α与β之比，与商品价格无关.

• α,β两种商品效用或消费者偏爱的度量.

推广到n种商品：

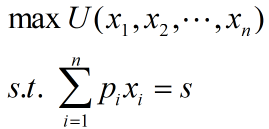
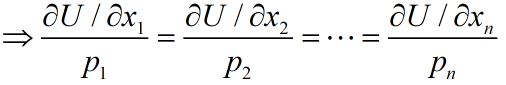
• 各种商品单位金额的边际效用相等时效用函数最大.

效用函数的几种常用形式：

（1）调和效用函数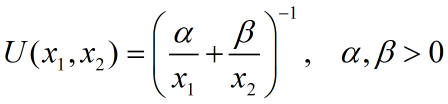

（2）幂效用函数

（3）均根方效用函数

效用最大化模型的应用：

• 问题：草莓、芒果和桔子每千克价格为15元,10元和5元,准备花100元采购,怎样分配这笔钱？

• p1, p2, p3 3种水果价格，x1, x2, x3 购买数量

• 效用最大化模型

  

  
  

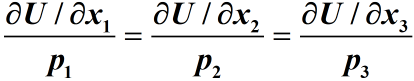
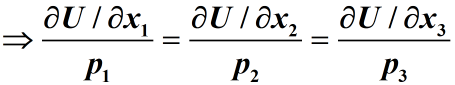
• 需确定3种水果的效用函数U(x1, x2,x3)或边际效用.

• 确定效用函数U(x1,x2,x3)或边际效用的办法

• 办法一：采用现成的效用函数表达式

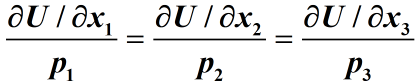
  按照α:β:γ 分配100元

  3种水果的效用或偏爱，α=6/10, β=1/10, γ=3/10

  60元买4kg草莓, 10元买1斤kg芒果, 30元买6kg桔子.

• 办法二

  给出每买1kg草莓,1kg芒果,1kg桔子效用函数的增加值(边际效用).

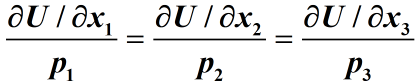
  p1=15, p2=10, p3=5, p1: p2: p3=3:2:1

  计算3种水果单位金额的边际效用：

•  按照3种水果单位金额边际效用从大到小的顺序，每次增加1kg购买量，直到花完准备付出的100元. 4kg草莓, 1kg芒果, 6kg桔子.

• 对办法一和办法二的分析

  办法一，购买量x1, x2, x3连续

  办法二，购买量离散

• 效用最大化的结果：“不买贵的，只买对的”！