4 数学规划模型
实际问题中的优化模型:
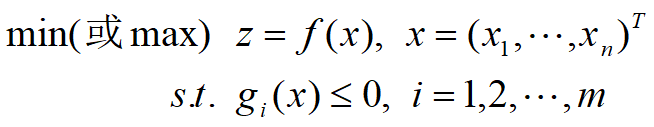
x ~决策变量,f(x) ~目标函数,gi(x)≤0 ~约束条件
多元函数条件极值:
决策变量个数n和约束条件个数m较大
最优解在可行域的边界上取得
数学规划:线性规划、非线性规划、整数规划
重点在模型的建立和结果的分析
4.1 奶制品的生产与销售
背景和问题:

每天:50桶牛奶,时间480小时,至多加工100千克A1
制订生产计划,使每天获利最大
35元可买到1桶牛奶,买吗?若买,每天最多买多少?
可聘用临时工人,付出的工资最多是每小时几元?
A1的获利增加到 30元/千克,应否改变生产计划?
模型建立:
决策变量:x1桶牛奶生产A1,x2桶牛奶生产A2
目标函数:每天获利
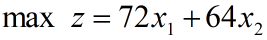
约束条件:
原料供应 ![]()
劳动时间![]()
加工能力 ![]()
非负约束 ![]()
线性规划模型(LP)
模型求解:软件实现LINGO
model:
max = 72*x1+64*x2;
x1 + x2<50;
12*x1+8*x2<480;
3*x1<100;
end
Global optimal solution found.
Objective value: 3360.000
Total solver iterations: 2
Variable Value Reduced Cost
X1 20.00000 0.000000
X2 30.00000 0.000000
Row Slack or Surplus Dual Price
1 3360.000 1.000000
2 0.000000 48.00000
3 0.000000 2.000000
4 40.00000 0.000000
20桶牛奶生产A1, 30桶生产A2, 利润3360元.
原料增加1单位, 利润增长48;时间增加1单位, 利润增长2;加工能力增长不影响利润
35元可买到1桶牛奶,要买吗? 35 <48, 应该买!
聘用临时工人付出的工资最多每小时几元? 2元!
敏感性分析 (“LINGO|Ranges” )
Ranges in which the basis is unchanged:
Objective Coefficient Ranges
Current Allowable Allowable
Variable Coefficient Increase Decrease
X1 72.00000 24.00000 8.000000
X2 64.00000 8.000000 16.00000
Righthand Side Ranges
Row Current Allowable Allowable
RHS Increase Decrease
2 50.00000 10.00000 6.666667
3 480.0000 53.33333 80.00000
4 100.0000 INFINITY 40.00000
x1系数范围(64,96),x2系数范围(48,72)
A1获利增加到 30元/千克,应否改变生产计划?
x1系数由24×3=72增加为30×3=90,在允许范围内,生产计划不变
35元可买到1桶牛奶, 每天最多买多少? 最多买10桶!


