5.6  传染病模型和SARS的传播

• 2002年冬到2003年春，一种名为SARS（Severe Acute Respiratory Syndrome，严重急性呼吸道综合症，民间俗称非典）的传染病肆虐全球。

• SARS首发于中国广东，迅速扩散到30多个国家和地区，多名患者死亡，引起社会恐慌、媒体关注，各国政府和联合国、世界卫生组织的高度重视、积极应对，直至最终控制住疫情的蔓延。

• SARS疫情持续时间2002.12-2003.07，累计感染人数8422(内地5327), 死亡人数919(内地349), 病死率11%.

• 近期发生的新冠肺炎（COVID-19）疫情是由一种新型冠状病毒感染引起的急性呼吸道传染病，疫情远比当年的SARS严重，目前疫情影响仍在继续，人们日常生活和学习均受到影响。

• 新冠肺炎疫情自2020年初爆发以来，迅速在全球大流行，给人类生命安全带来了严峻的挑战，截至2022年3月23日，世卫组织网站最新数据显示，全球确诊病例达到4.73亿人。当下，已肆虐两年之久的新冠疫情仍没有终结迹象。

• SARS被控制住不久，2003年9月全国大学生数学建模竞赛以“SARS的传播”命名当年A题和C题。

赛题要求：

• 建立你们自己的模型；特别要说明怎样才能建立真正能预测以及能为预防和控制提供可靠、足够信息的模型，这样做的困难在哪里? 

• 对于卫生部门所采取的措施做出评论，如：提前或延后5天采取严格的隔离措施，对疫情传播所造成的影响做出估计。

• 北京市从2003年4月20日至6月23日逐日的疫情数据（参见后面的阅读文档）。

传染病模型和SARS的传播：

• 介绍数学医学领域中基本的传染病模型。

• 结合赛题介绍几个描述、分析SARS传播过程的模型及求解结果。

1、基本的传染病模型

背景和问题：

• 描述传染病的传播过程

• 分析受感染人数的变化规律

• 预报传染病高潮到来的时刻

• 探索预防传染病蔓延的手段

• 不从医学角度分析各种传染病的特殊机理

• 按照传播过程的规律建立微分方程模型

模型一：SI模型

将人群分为两类：易感染者(Susceptible，健康人)和已感染者(Infective,患者).

假设：

1. 总人数N不变，时刻t 健康人和患者所占比例分别为s(t)和i(t),有s(t)+i(t)=1.

2. 每个患者每天有效接触人数为λ，称接触率，且当健康人被有效接触后立即被感染成为患者，λ也称感染率。

建模：

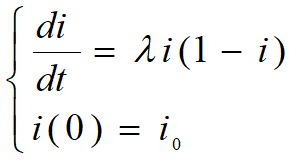
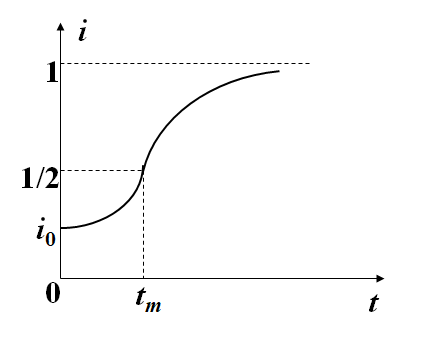
  Logistic 模型

，  

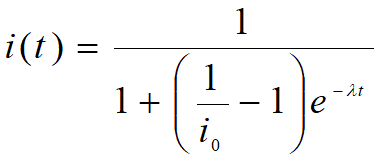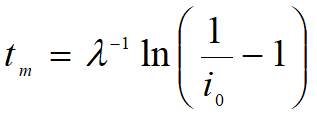
t=tm, di/dt 最大，tm~传染病高潮到来时刻

λ (感染率)↓  tm↑

?  没有考虑病人可以治愈！

模型二：SIS 模型

传染病无免疫性如伤风、痢疾等——患者治愈成为健康人，健康人可再次被感染。

增加假设：3.患者每天治愈的比例为μ(治愈率)

建模：

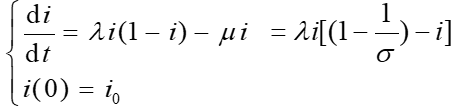
，λ ~感染率，1/μ~感染期

σ  ~整个感染期内每个患者有效接触而感染的平均（健康）人数，称为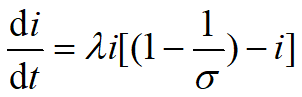感染数。

， ~感染数

  ；

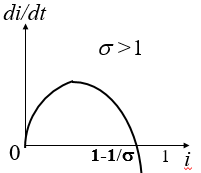
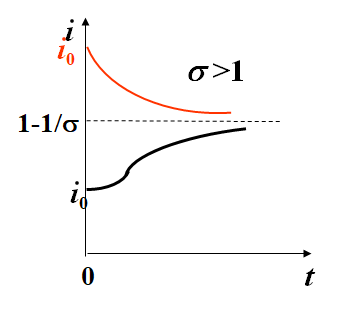
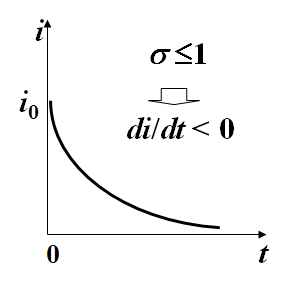
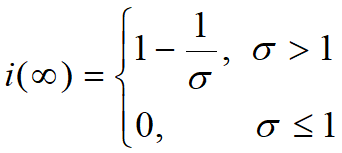
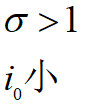
• 接触数σ =1~ 阈值，若每个患者在生病期间因有效接触而感染的人数大于1，则患者比例增加；反之，减少。

• SI模型如何看作SIS模型的特例？

模型三：SIR模型

• 传染病有免疫性如天花、流感、麻疹等——患者治愈后移出感染系统。

• 传染病模型中将病愈免疫后和因病死亡的人称为移除者(Removed).

假设：

1. 总人数N不变，健康人、患者和移除者的比例分别为s(t), i(t), r(t).  

2. 感染率为λ,治愈率为μ（因包含死亡，实际上是移除率）,感染数σ =λ/μ.

建模：，需建立两个方程.

， 

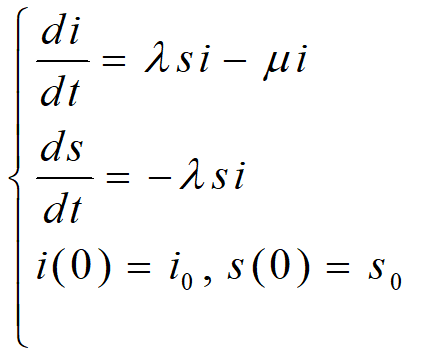
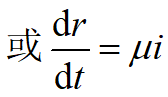• 关于i(t) , s(t)的非线性微分方程组，没有解析解，

  只能通过数值计算得到s(t), i(t), r(t)的曲线.

• 在相平面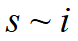上研究解的性质：

  消去dt，得   

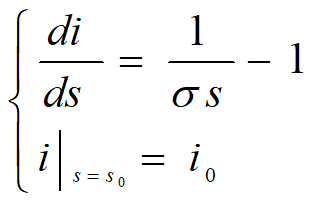
• 相轨线

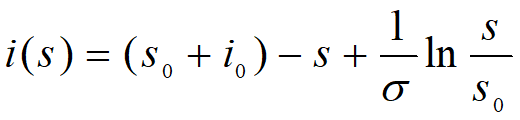
  定义域

  在D内作相轨线的图形，进行分析

• 相轨线及其分析

      s(t)单调减®相轨线的方向

      ，

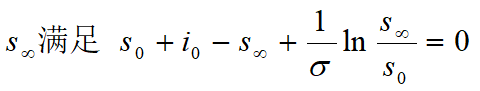
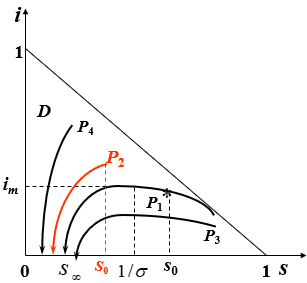
      P1: s0>1/σ →i(t)先升后降至0传染病蔓延

      P2: s0≤1/σ →i(t)单调降至0传染病不蔓延

     —— 1/σ ~阈值

• 预防传染病蔓延的手段：

  传染病不蔓延的条件—— s0≤1/σ

• 提高阈值1/σ 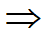 降低σ (=λ/μ) 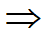λ ↓, μ­↑

      λ (感染率)↓  卫生水平­­­­­­­­­­↑

     μ (治愈率)­↑­ 医疗水平­­↑

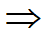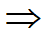• 降低 s0 提高 r0 群体免疫

• σ 的估计：，

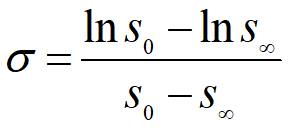
• 被传染人数比例的估计

SIR模型的数值计算：

设s(0)=0.99, i(0)=0.01

健康人s(t), 患者i(t),移除者r(t).接触率λ,治愈率μ . 

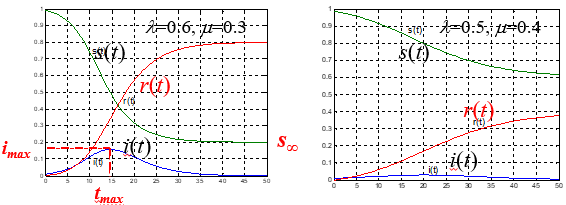
    s(t)单调减,r(t)单调增,都趋于稳定,i(t)先增后减趋于0.

    s∞～最终未被感染的比例

    imax(tmax)～传染病高潮时的比例

 ——衡量传染病传播的强度和速度

结果分析：感染率λ,治愈率μ.

 1/μ ～平均传染期(患者被治愈所需平均时间)

    σ=λ/μ ～感染数(感染期内每个患者有效接触而感染的人数)

 卫生水平高Þ感染率λ小；医疗水平高Þ治愈率μ大

 感染数σ=λ/μ 小——有助于控制传播.

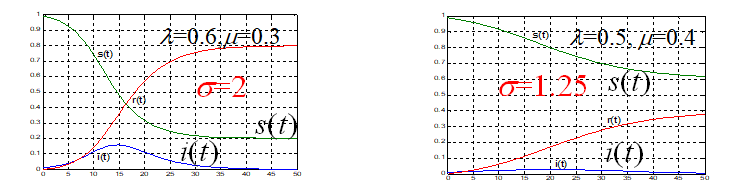
 感染数σ变小

 健康人比例s(t)更大, 患者比例i(t)更小.

 健康人s(t), 患者i(t). σ=l/μ ～感染数.

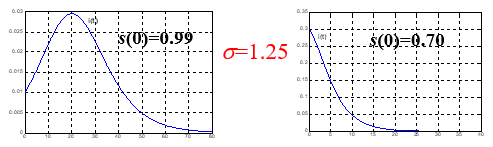
    σs(0)>1，i(t)先增后减～传染病蔓延

    σs(0)≤1，i(t)单调减少～传染病不蔓延

• 一般情况下s(0)≈1, 控制蔓延需要σ<1——提高卫生水平和医疗水平！

• 预防接种使群体免疫,提高r(0)使s(0)减小,满足σs(0)≤1.

注：实际传播过程中，参数λ和μ并不如上述假定是常数，而会随预防措施的加强和医疗水平的提高而发生较大变化。

2、SARS 的传播模型

• 2003年SARS爆发初期，处于几乎不受制约的自然传播形式，后期的传播则受到严格控制。

• 虽然影响因素众多，不只有健康人、患者、移除者3个人群，但是仍然可以用愈后免疫的SIR模型来描述。

• 越复杂的模型包含的参数越多，为确定这些参数所需要的疫情数据就越全面，而实际上能够得到的数据是有限的。

模型一  参数时变的SIR模型

模型构造：

• s(t), i(t), r(t)~ 第t天健康人、患者、移除者(病愈与死亡之和)的数量， s(t)+i(t)+r(t)=N.

• λ(t), μ(t) ~第t天感染率, 移除率(治愈率与死亡率之和).

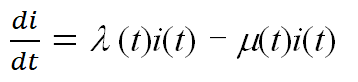
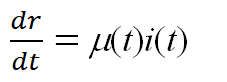
 ——参数时变的SIR模型

参数估计与拟合：确诊-r(t)=i(t)，死亡+治愈=r(t)

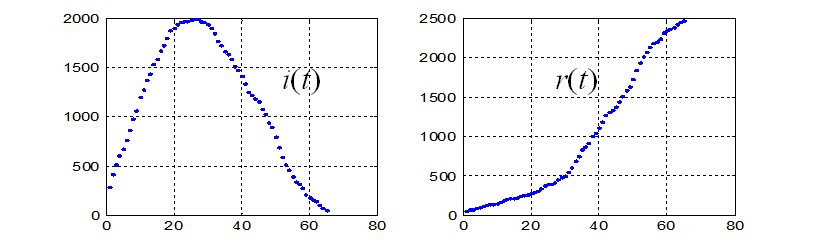
• 取差分近似导数：m(t)=Δr(t)/i(t)，l(t)=(Δi(t)+Δr(t))/i(t)

• 用t=1~20的数据拟合得

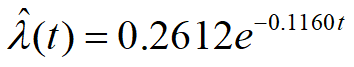
  用t=20~50的数据拟合得

• 代入方程组，求i(t)，r(t)的数值解

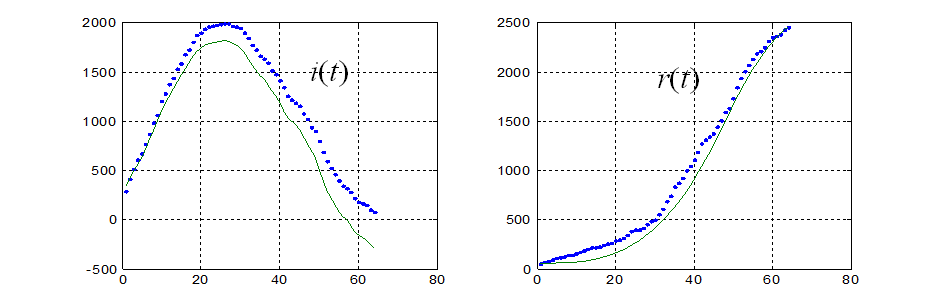
• i(t)的计算值整体偏小，且t=50后下降过快。

• 在模型构造、参数拟合等方面仍需改进。

模型二  引入不可控带菌者和疑似已感染者的模型

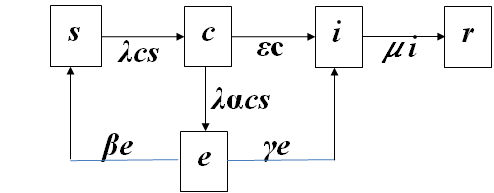
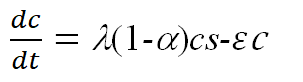
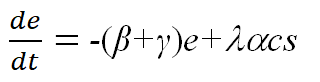
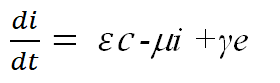
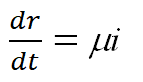
• 参数λ, μ, ε, α, β, γ确定后，由任意5个方程及任意4个初值计算5类人群的比例s(t), c(t), e(t), i(t), r(t).

参数估计：

• 直接利用实际数据。
  

• 由经验估计初值，代入模型计算，根据计算值与实际值的偏差调整估计值。

模型三  引入尚未隔离和已经隔离已感染者的模型

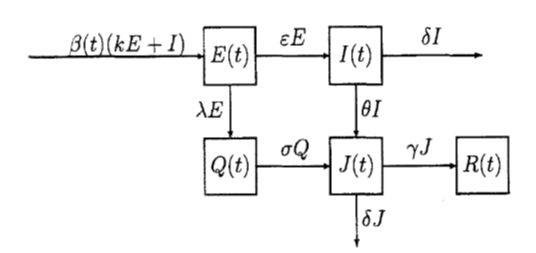
小结与评注：

• 在SIR模型基础上建立的各具特色的微分方程模型，差别在于人群划分和参数定义。

• 模型求解结果是否与实际吻合的关键在参数估计，而参数估计的结果依赖于是否有充分的数据。

• 人群的细分必然要引进更多的参数，如果参数很难估计，即便模型很精细也得不到好的结果。

• 传染病传播过程中的参数大多是变化的，应根据数据拟合出参数的时间函数，再用模型计算。