5.3  经济增长模型

发展经济，提高生产力的主要手段——增加投资，增加劳动力，技术革新（本案例中暂不考虑）

• 建立产值与资金、劳动力之间的关系

• 研究资金与劳动力的最佳分配，使创造的效益最大

• 调节资金与劳动力的增长率，使经济(生产率)增长

1. 道格拉斯(Douglas)生产函数

• 产值 Q(t)Ü 资金 K(t)，劳动力 L(t)

      ，F为待定函数

• 静态模型

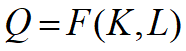
• 每个劳动力的产值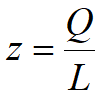；每个劳动力的投资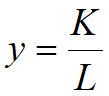

模型假设：z 随着 y 的增加而增长，但增长速度递减

       ，

     ——Douglas生产函数

• ，
  

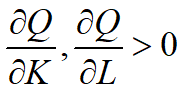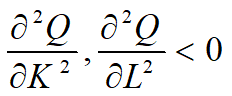
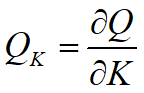• ~ 单位资金创造的产值

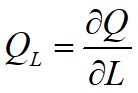       ~ 单位劳动力创造的产值

• a ~资金在产值中的份额，1-a ~劳动力在产值中的份额

• 更一般的道格拉斯(Douglas)生产函数

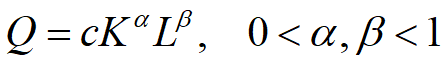
2. 资金与劳动力的最佳分配（静态模型）

• 资金来自贷款，利率 r，劳动力需付工资 w

  资金和劳动力创造的效益

• 求资金与劳动力的分配比例K/L(每个劳动力占有的资金) ，使效益S最大

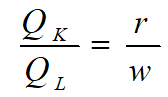
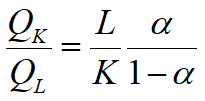
• w ↑­,  r ↓,  a ­↑  Þ K/L­ ↑

3. 经济(生产率)增长的条件(动态模型)

• 要使 Q(t) 或 Z(t)=Q(t)/L(t)增长,  K(t), L(t)应满足的条件

模型假设：

• 投资增长率与产值成正比(用一定比例扩大再生产)

  Þ

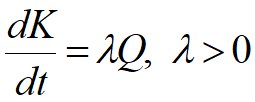
• 劳动力相对增长率为常数

       Þ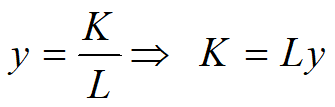Þ

  Þ，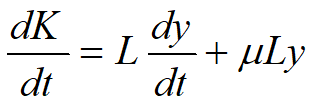

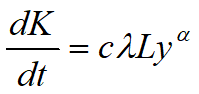
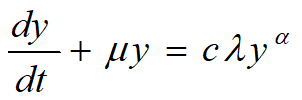• ——Bernoulli方程

     求解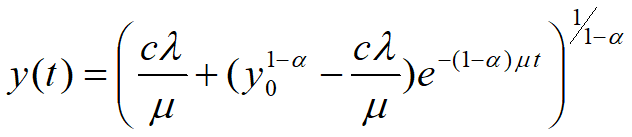

  Þ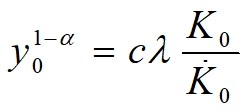

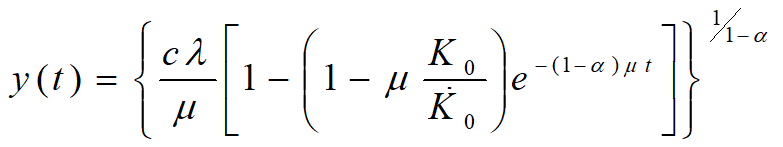
• 经济增长的条件

（1）产值Q(t)增长 Û dQ/dt > 0

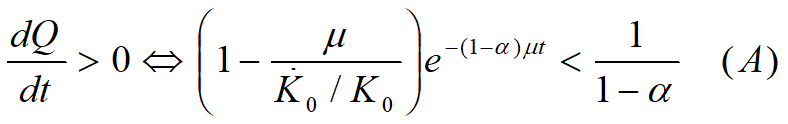
  当

  当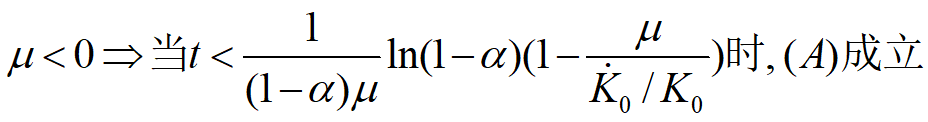

    ——说明如果劳动力减少，Q(t)只能在有限时间内保持增长

（2）每个劳动力的产值Z(t)=Q(t)/L(t)增长 Û dZ/dt>0

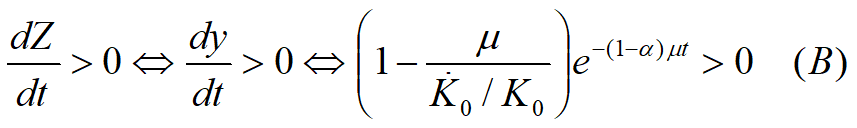
 当

 当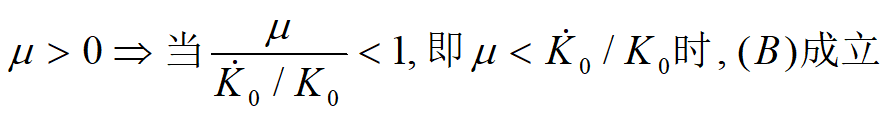

   ——劳动力增长率小于初始投资增长率