5 微分方程模型
微分方程～含自变量、未知函数及其导数的方程.
描述随时间连续变化物体或过程的动态变化规律.
采用机理分析方法或类比法建立微分方程.
物理领域～工程技术,科学研究：牛顿定律，电路原理
例.火箭发射——由燃料燃烧推力发射的火箭加速度、速度、高度的微分方程.
非物理领域～人口,经济,生态等：特定的内在规律
例.人口预测——含人口数量及增长率的微分方程.
5.1 人口模型
背景和问题：
研究人口变化规律，控制人口过快增长
建立数学模型描述人口发展规律，是制定积极、稳妥人口政策的前提.
①介绍两个基本的人口模型
②用美国人口数据估计参数
③模型检验和增长预测
美国人口统计数据（单位：百万）
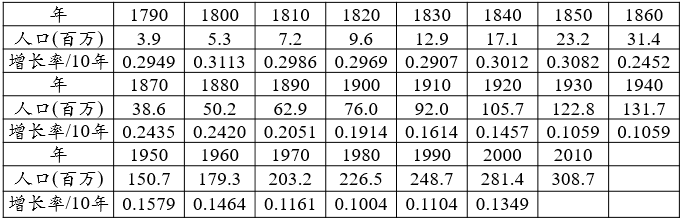
模型建立和求解：
1. 指数增长模型
①一个常用的人口预测公式
今年人口x0,年增长率r，k年后人口
基本前提～增长率r在k年内保持不变.
已知增长率预测未来人口.
根据人口统计数据估计增长率——由x0, xk估计r.
例. 从1960年到1999年( 39年时间)世界人口翻番.
该期间的年平均增长率约为 r=(ln2)/39=1.8% 为什么？
②人口指数增长模型的建立——马尔萨斯1798年提出
假设：
t时刻人口数量为连续、可微函数x(t).
单位时间人口增长率为常数r.
初始时刻(t=0)的人口为x0
模型：
单位时间内x(t)的增量为rx(t)
Þ
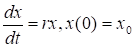，其解
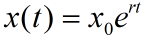
解释：
与常用公式一致?
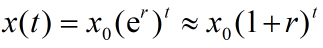
t→∞,x(t)→∞,人口按指数规律无限增长?
③指数增长模型的参数估计 (数据拟合)
方法一：直接用人口数据和线性最小二乘法.
根据1790年 (t=0)至2000年美国人口数据
最小二乘法，MATLAB编程计算
Þ r=0.2020/10年，x0=6.0496
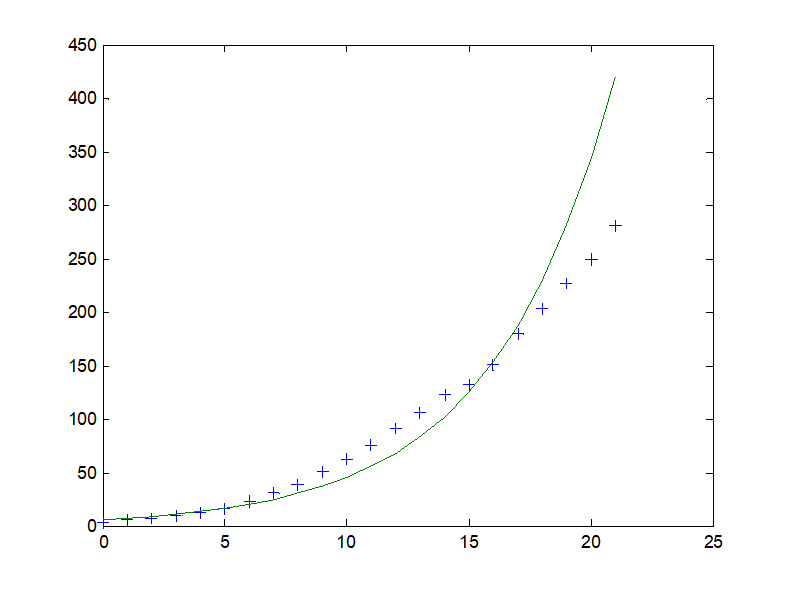
方法二：对人口数据作数值微分估计增长率.
设x(t)在t0, t1, …, tn(等间距△t)的函数值为x0, x1, …, xn
Þ x(t)在各点的导数近似值——数值微分中点公式
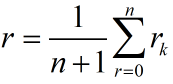
Þ r=0.2052/10年，x0=3.9 (原始数据)
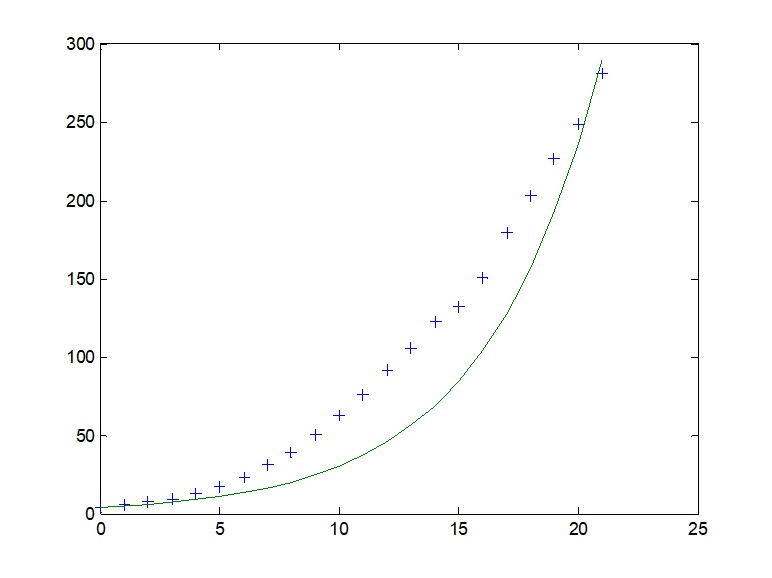
④改进的指数增长模型
修改人口增长率为常数的假设.Þ r(t)=r0-r1t
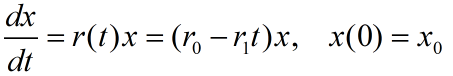Þ 
根据10年增长率数据，线性最小二乘法
Þ r0=0.3252，r1=0.0114，x0=3.9 (原始数据)
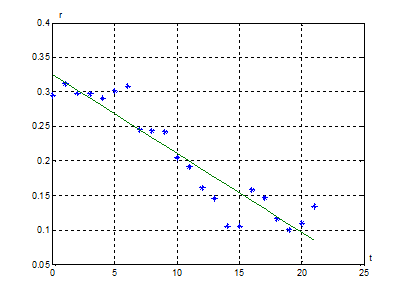
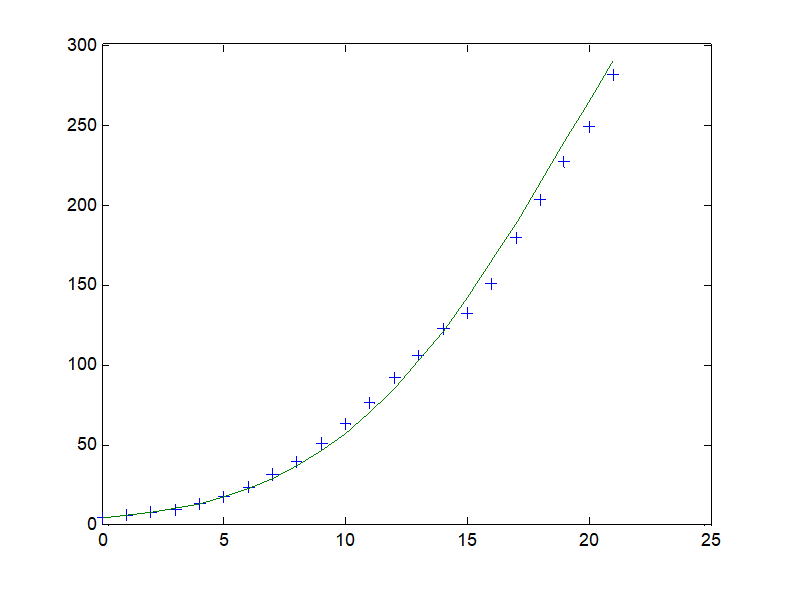
⑤美国人口用指数增长模型计算结果的比较
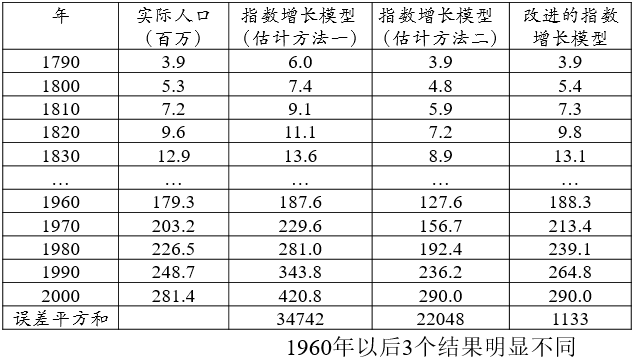
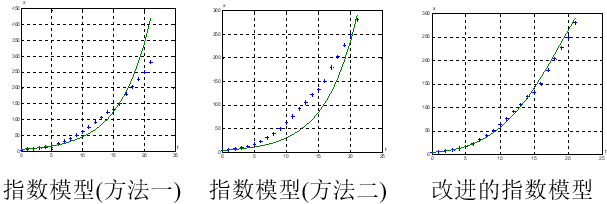
用指数模型计算的美国人口与实际数据相差很大.
200多年时间内假设增长率为常数违背实际情况.
⑥指数增长模型的应用及局限性
与19世纪以前欧洲一些地区人口统计数据吻合
适用于19世纪后迁往加拿大的欧洲移民后代
不符合19世纪后多数地区人口增长规律
可用于短期而不能用于较长期的人口预测.
改进的指数模型计算结果有所改善, 但它未反映增长率下降的机理, 函数形式也不易确定, 不便于应用.
19世纪后人口数据
人口增长率r不是常数(逐渐下降)需分析人口增长率下降的机理,修改假设建立新模型.
2. logistic模型
模型建立：
人口增长到一定数量后，增长率下降的原因：资源、环境等因素对人口增长的阻滞作用且阻滞作用随人口数量增加而变大
r是x的减函数假设
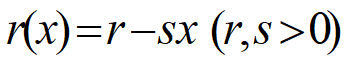，r～固有增长率(x很小时)，xm～人口容量（资源、环境能容纳的最大数量）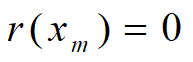
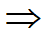
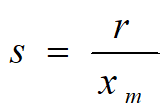Þ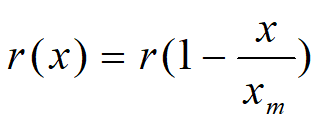
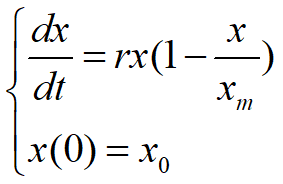
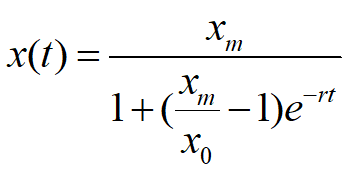
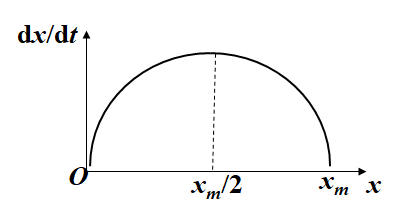
rx～人口自身增长，(1-x/xm)～资源和环境阻滞人口增长
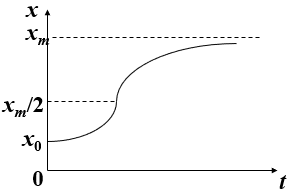
x(t)~ S形曲线,x 增加先快后慢
参数估计：
方法一：数值微分计算增长率,线性最小二乘估计参数.
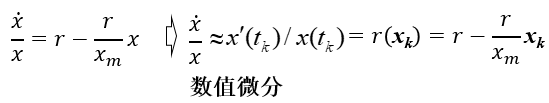
线性最小二乘法
r=0.2805/10年，xm=352.0548，x0=3.9 (原始数据)
方法二：直接用数据和非线性最小二乘估计参数.
r=0.2155/10年, x0= 7.6962,xm=443.9931
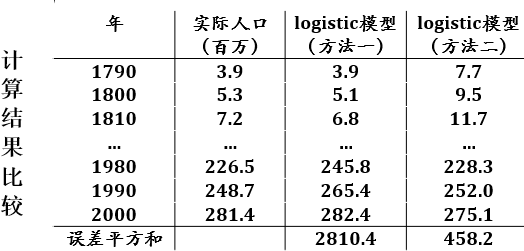
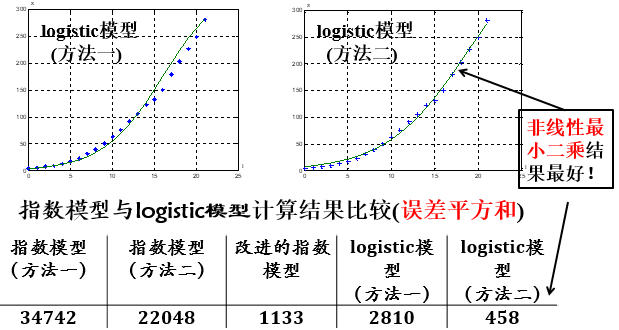
对1790年至2000年美国人口数据的拟合，logistic模型比指数增长模型有很大改善.
模型检验和人口预测：
上面表、图给出的结果是利用1790年至2000年美国人口数据估计的参数代入模型计算得到的.
这些结果与同期实际数据比较虽能反映模型与数据的拟合程度, 但不是真正意义上的模型检验.
在估计指数模型和logistic模型参数时未用2010年的美国人口，留下这个实际数据用于模型检验.
用1790年至2000年美国人口估计参数代入模型,计算2010年人口与实际值比较作为模型检验.
2010年实际人口加入重估参数预测2020年人口.
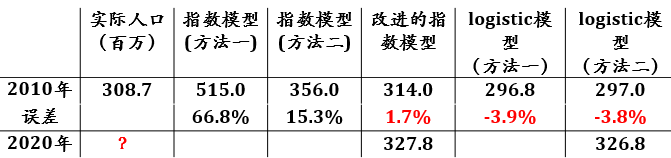
模型检验的误差在5%以内，可以接受.
预测准确性需等2020年美国人口调查结果公布.拭目以待！
logistic模型的广泛应用：
logistic模型~欧洲生物数学家Verhulst19世纪提出，中译名为逻辑斯谛.
生态、医疗领域中的应用——鱼塘中鱼群数量、森林中树木数量、传染病传播人数的变化规律.
经济、社会领域中的应用——耐用消费品销售量、消息传播范围的变化规律.
