6.3  市场经济中物价的波动

背景和问题

消费者在自由竞争的市场经济中常会遇到商品价格的波动现象.

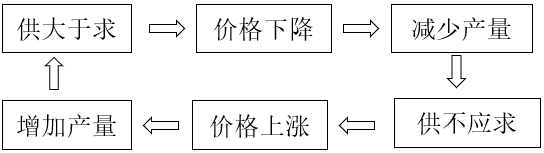
• 商品数量和价格主要由供求关系决定.

  供求平衡商品数量和价格基本稳定.

  供求失衡商品数量和价格出现波动.

• 波动的两种形式

  振幅逐渐减小，最终趋向平稳.

  振幅越来越大，如不干预将导致经济崩溃.

• 建立数量—价格模型，描述波动现象，研究趋向平稳的条件，讨论政府的干预方式.

模型假设    时段~生产周期 (饲养周期、种植周期)

    xk~ 第k时段商品数量；yk ~ 第k时段商品价格.

 1. 供求关系平衡商品数量x0和价格y0保持不变 

 2. yk由消费者需求关系决定：xk>x0, 供过于求yk<y0

 3. xk+1由生产者供应关系决定：yk<y0, 价格过低xk+1<x0

 4. xk, yk偏离x0, y0不大时, 偏离yk-y0与xk-x0成正比,偏离xk+1-x0与yk-y0成正比.

差分方程模型

  由假设2，xk>x0yk<y0；由假设4，yk-y0与xk-x0成正比

  由假设3，yk<y0 xk+1<x0；由假设4，xk+1-x0与yk-y0成正比

      ——xk,yk的差分方程组

  消去yk-y0得——xk的差分方程模型

      xk递推至x1得

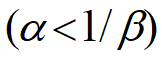
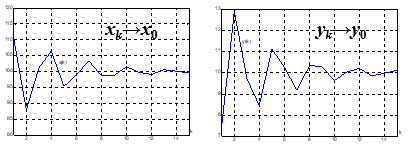
• xk→x0，yk→y0，x0,y0稳定

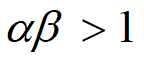
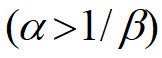
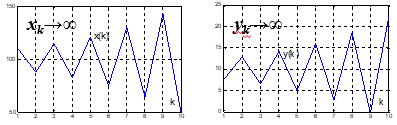
• xk,yk→∞，x0,y0不稳定

模型分析

例. 平衡状态：x0=100, y0=10(元).

  数量减少1价格上涨0.1元α =0.1      

  价格上涨1元下一时段供应量增加5β=5

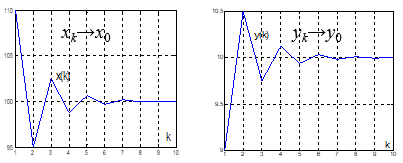
      x0,y0稳定

      α=0.24，β =5

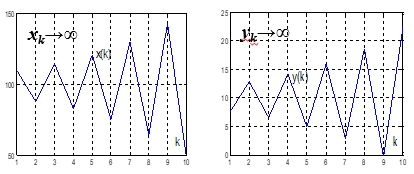
      x0,y0不稳定

模型分析

        α~商品数量减少1单位, 价格上涨幅度

         β ~价格上涨1单位, (下时段)供应的增量

• α~ 消费者对需求的敏感程度，α小, 有利于经济稳定

• β~ 生产者对价格的敏感程度，β小, 有利于经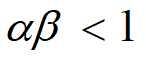济稳定

• 经济稳定

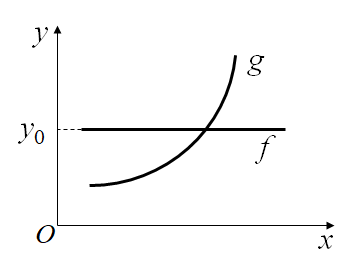
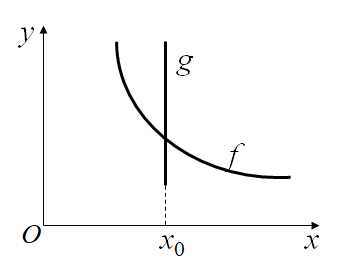
蛛网模型  差分方程模型的图形表示

• xk~第k时段商品数量  yk ~第k时段商品价格

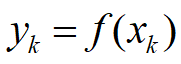
• 消费者的需求关系需求函数减函数

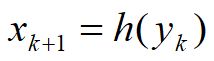
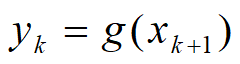
• 生产者的供应关系供应函数增函数

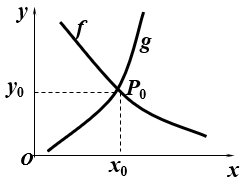
• f 与g的交点P0(x0,y0) ~ 平衡点

  一旦xk=x0，则yk=y0,且xk+1=xk+2=…=x0, yk+1=yk+2= …=y0                     

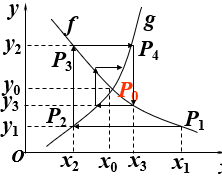
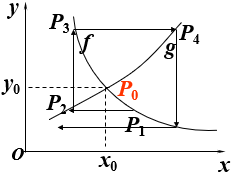
• 如左图：设x1偏离x0，

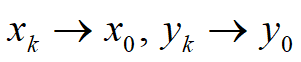
       P0是稳定平衡点

  曲线斜率（斜率取绝对值）

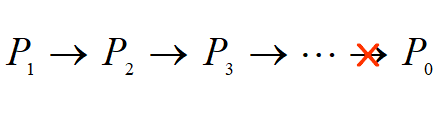
• 如右图：P0是不稳定平衡点

  曲线斜率

  
  

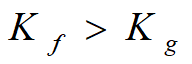
差分方程模型与蛛网模型的一致性

• 差分方程模型：在P0点附近用直线近似曲线

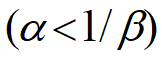
• xk→x0，yk→y0，x0,y0稳定

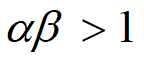
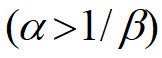
• xk,yk→∞，x0,y0不稳定

• 蛛网模型：

      ，P0是稳定平衡点

      ，P0是不稳定平衡点

• 方程模型与蛛网模型的一致：，

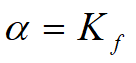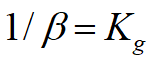
经济不稳定时政府的干预办法：

• 稳定平衡

           

1. 使α尽量小，如α =0需求曲线变为水平

• 以行政手段控制价格不变

2. 使β尽量小，如β =0供应曲线变为竖直

• 靠经济实力控制数量不变

差分方程模型的推广

  消费者需求关系不变

  生产者管理水平和素质提高

• 根据当前和前一时段的价格决定下一时段的产量.
  

  ——xk，yk的差分方程组

• 已知α,β及x0, y0, 由初始值x1, x2递推地计算xk,yk.

• α =0.24,β =5 不变

  原模型，αβ =1.2>1，x0, y0不稳定

      新模型，αβ =1.2>1，x0, y0稳定

• 讨论稳定条件

        ，

           ——二阶线性常系数差分方程

            l1, l2～特征根，~ 特征方程

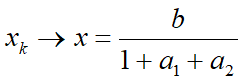       ，~ 稳定平衡点

   特征方程

• 稳定条件(xk→x0):½l1½, ½l2½<1

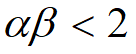
   比原模型的稳定条件放宽了.

          生产者管理水平和素质的提高有利于经济稳定！

小结与评注

• 对市场经济中“供不应求价格上涨、供过于求价格下跌”的现象用两种模型描述和解读：差分方程：便于运算；蛛网模型：直观鲜明

• 模型参数有明确的经济学含义——敏感系数.

• 政府干预措施具有人们熟知的现实背景.

• 差分方程平衡点的稳定性有明显的实际意义，反映了数学与现实的密切关系.