6.2  管住嘴迈开腿

背景和问题：

• 测评体重的标准——体重指数(BMI Body Mass Index)

  BMI=w / l2，w～体重(kg), l身高(m).

  18.5<BMI<24.9 ~ 正常；25<BMI<29.9 ~ 超重；BMI≥30 ~ 肥胖.

  例： l=1.70m， w=63.5 kg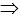，BMI=22  标准的身材

               l=1.70m， w=100 kg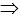，BMI=34.6  肥胖

• 多数减肥食品达不到减肥目标，或不能维持.

• 通过控制饮食和适当的运动，在不伤害身体的前提下，达到减轻体重并得以控制的目的.

模型分析：

• 人体通过食物摄入热量,通过代谢和运动消耗热量.

  二者平衡,体重不变；平衡被破坏则体重变化.

• 分析对热量的吸收和消耗, 建立体重变化规律的模型.

• 减肥计划应以不伤害身体为前提.吸收热量不过少、减少体重不过快.

• 增加运动量是加速减肥的有效手段.

• 以周为时间单位制订减肥计划，建立差分方程模型.

模型假设：

1）体重增加正比于吸收的热量——每8000 kcal 增加体重1 kg；

2）代谢引起的体重减少正比于体重——每周每千克体重消耗200 ~ 320 kcal (因人而异), 相当于70 kg 的人每天消耗2000 ~ 3200 kcal；

3）运动引起的体重减少正比于体重，且与运动形式有关；   

4）为了安全与健康, 每周吸收热量≥10000kcal,且每周减少量≤1000kcal,每周体重减少量≤1.5kg.

调查资料：

基本模型：

• w(k) ~ 第k周(末)体重(kg) , k=1,2,…，c(k) ~第k周吸收热量(kcal)，a =1/8000 (kg/kcal) ~ 热量转换系数，b ~ 代谢消耗系数(因人而异)

• 由b和吸收热量c(k)决定体重w(k)的变化规律.

减肥计划的提出：

• 某人身高1.70m, 体重100kg, BMI高达34.6. 目前每周吸收20000 kcal热量，体重维持不变. 

• 制订减肥计划使体重减至75kg(BMI=26)并维持下去.

  1. 在正常代谢情况下安排一个两阶段计划:

第一阶段：吸收热量每周减少1000kcal, 直至达到安全下限10000 kcal/周；

第二阶段：每周吸收热量保持下限, 达到减肥目标 .

  2. 为加快进程而增加运动，重新安排两阶段计划.

  3. 给出达到目标后维持体重不变的方案.

减肥计划的制定：

1. 确定某人的代谢消耗系数b

  每周吸收20000kcal, 体重100kg不变.

   由基本模型，令

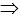
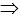
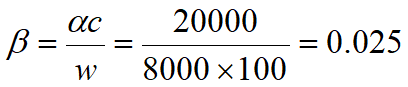
• 每周每千克体重消耗20000/100=200kcal——某人正常代谢消耗相当弱.

2. 正常代谢情况下的第一阶段计划

• 吸收热量由20000kcal每周减少1000kcal, 直至达到安全下限10000 kcal/周.
  

         ，

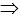
         第一阶段需10周

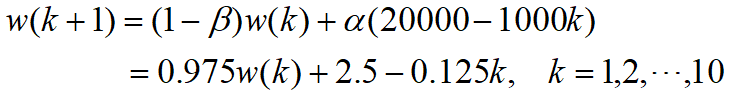
3.正常代谢情况下的第二阶段计划

• 吸收热量保持下限cmin=10000kcal/周,体重减至75kg.

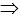
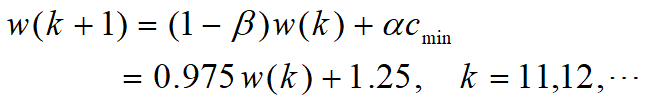
• 第二阶段需22周.

• 两阶段计划共需32周.

4. 为加快进程而增加运动

  t ~每周运动时间(h)，γ ~运动每小时每千克体重消耗热量

      β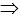β+αγt，

  取 γt =40(如每周步行7h加乒乓4h)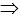β+αγt=0.03

• 第二阶段缩短为12周，两阶段计划共需22周.

5.检验“每周体重减少量≤1.5kg”

 正常代谢

 增加运动

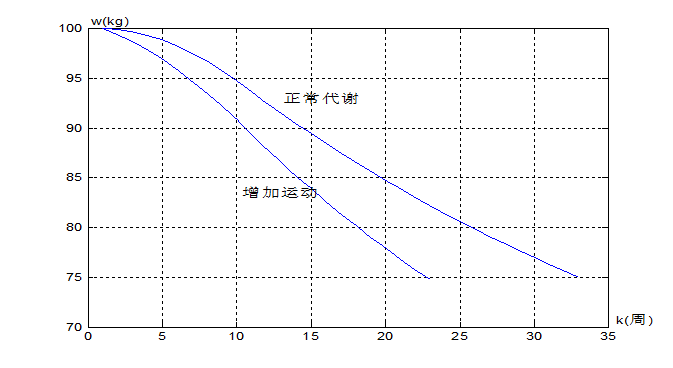
  编程计算w(k)，可见满足

6. 达到目标后维持体重不变的方案

• 每周吸收热量保持常数c使体重w=75kg不变.

• 正常代谢

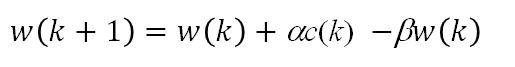
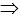
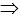
        =15000kcal/周

• 若增加 γt =40的运动，则c=18000kcal/周

• 若减肥计划的开始，就让c由20000kcal/周直接减至15000,14000,13000,12000时体重w(k)下降曲线.

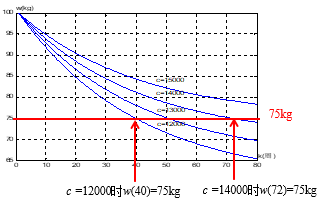
• 比两阶段计划的时间长，吸收热量突减对身体不利.

7. 达到目标体重所需时间与每周吸收热量的关系

      k=1递推至k=n

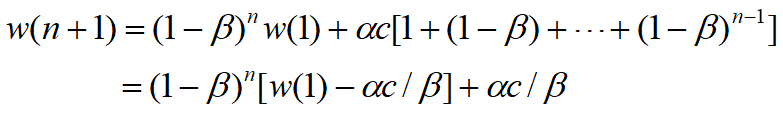
  令目标体重w*=w(n+1),记初始体重w1= w(1)

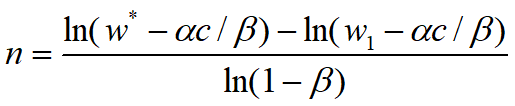
  c=14000，n=70.7707；c=12000，n=38.7407

小结与评注：

• 减肥科学化、定量化——需要研究人体体重变化的规律.

• 体重变化既有普遍规律也与每个人特殊生理条件有关，特别是代谢消耗系数β.

• 计算中由于增加运动使β由0.025提高到0.03时(变化20%),减肥所需时间从32周减少到22周(变化约30%)——体重变化对β相当敏感.