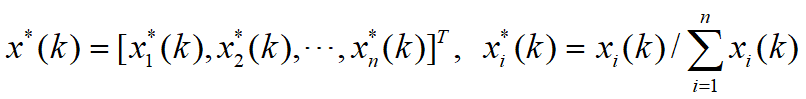6.4 动物的繁殖与收获
背景和问题:
野生动物种群在自然环境下繁殖、成长、死亡,不同年龄动物的数量比例保持平衡.
饲养动物种群在人类控制下,使不同年龄动物的数量比例达到稳定的预期目标.
建立动物种群的自然增长模型;讨论饲养动物种群的稳定收获.
按年龄分组的动物种群增长模型:
不同年龄动物的繁殖率、死亡率差别较大.
按照年龄分组,时段与年龄组相对应.
种群通过雌性繁殖而增长
以雌性个体数量为对象,总体数量按性别比计算.
建立按年龄分组种群增长的差分方程模型.
讨论稳定状况下种群的增长规律.
模型假设:
种群按照年龄等间隔地分为n个年龄组.
时间分成与年龄组区间大小相等的时段.
在稳定环境下和不太长时期内,
每个年龄组的雌性个体在一个时段内的繁殖率和死亡率不随时段变化.
模型建立:
xi(k)~第i年龄组第k时段的种群数量,i=1,2,…,n,k=0,1,2,…
bi~第i年龄组的繁殖率(每个雌性个体一个时段繁殖的数量).bi≥0,至少一个bi>0.
di ~第i年龄组的死亡率(一个时段内死亡数量在总量中的比例).
si=1-di ~存活率. 0<si≤1, sn=0
第1年龄组(出生婴儿)k+1时段数量=各年龄组k时段繁殖数量之和.
![]()
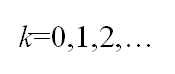
k时段第i年龄组存活的部分到k+1时段演变为第i+1年龄组.
![]()
![]()
![]()
——n个变量的差分方程组
已知bi,si及xi(0)
任意时段各年龄组的种群数量
——按年龄分组的种群增长模型
模型建立:
![]() ,
,![]()
记
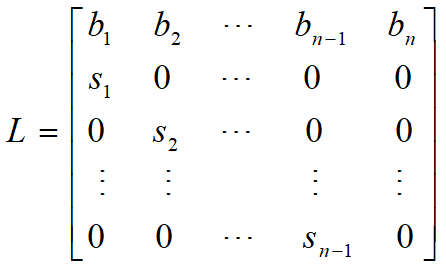 ,
,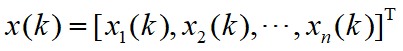
按年龄分组的种群数量
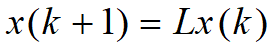
![]() ——Leslie模型
——Leslie模型
—— x(k)的归一化向量,按年龄分组的分布向量.
模型求解:
例. 种群分5个年龄组, 繁殖率为b1=0, b2=0.2, b3=1.8, b4=0.8, b5=0.2, 存活率为s1=0.5, s2=0.8, s3=0.8, s4=0.1, 各年龄组初始数量均为100只.
求任意时段各年龄组数量x(k)及分布向量x*(k).

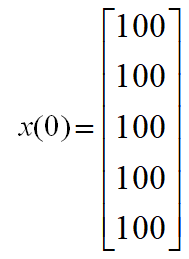
![]() ,
, ![]()

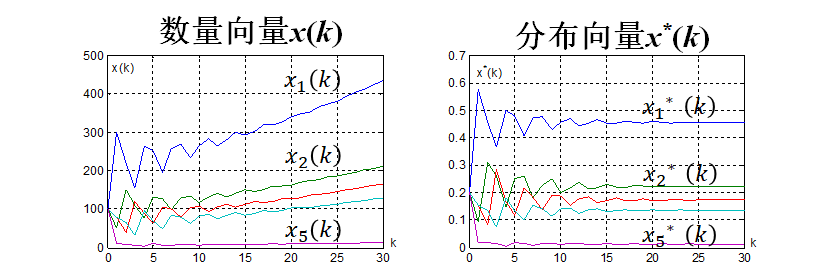
k充分大,x(k)仍在增长 x*(k)趋向稳定
按年龄分组的种群增长模型及MATLAB求解,举例
结果分析:
分析k充分大后x(k),x*(k)的变化规律
稳定状态分析的数学知识
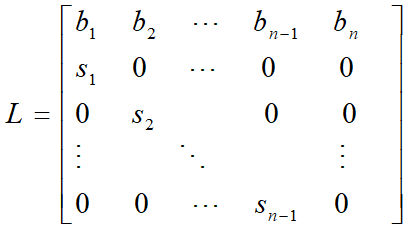
矩阵L存在最大特征根λ(正单根)
λ对应特征向量xλ,
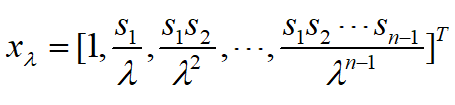
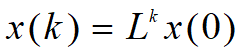 满足
满足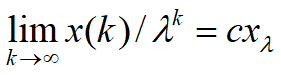 ,c~常数
,c~常数
k充分大x(k),x*(k)的特性
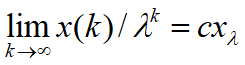
特征向量
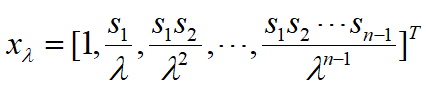
1.分布向量![]() ~ 稳定分布.与初始分布无关.
~ 稳定分布.与初始分布无关.
2.数量![]()
![]()
各年龄组数量按同一倍数λ(固有增长率)增减.
λ=1各年龄组数量保持不变.
3. λ=1时x(k)≈ cxλ,![]()
![]() ,si等于同一时段相邻年龄组的数量比.
,si等于同一时段相邻年龄组的数量比.
用算例验证x(k),x*(k)的特性

1.由L计算得到 λ=1.0254,
x*=[0.4559, 0.2223, 0.1734, 0.1353, 0.0132]T
模型求解中x*(30)近似于x*
2. 模型求解中xi(30)与xi(29)之比约为 λ=1.0254.
3. λ=1.0254比1略大, xi+1(30)与xi(30)之比近似于si
饲养动物种群的持续稳定收获模型:
控制饲养动物各年龄组的数量, 实现持续稳定收获:
即同一年龄组种群的收获量在每个时段都相等.
实现方法:每个年龄组每个时段种群的增长量=同一时段的收获量.
种群数量始终不变.
假定自然环境下饲养动物仍服从种群增长模型:
xi(k)~第i年龄组第k时段的种群数量.
![]() ,
,![]()
模型建立:
种群增长模型
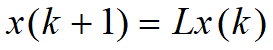
hi~第i年龄组种群的收获系数(收获量与总量之比)
增长量= 收获量
![]()
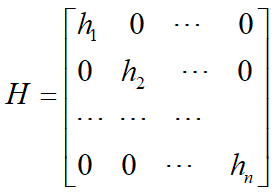
![]()
![]()
实现持续稳定收获——种群数量x(k)=x(对k不变)
![]()
![]()
![]() 最大特征根为1
最大特征根为1
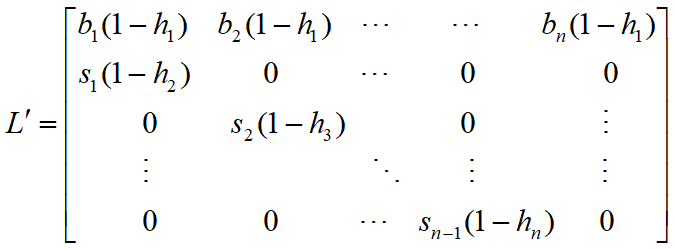
![]()
![]()
给定bi,si,选择收获系数hi,由上式,可得持续稳定收获
 ~ 种群数量的稳定分布:
~ 种群数量的稳定分布:
![]()
增长量= 收获量
由
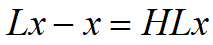
收获量的稳定分布
模型求解:
持续稳定收获的条件
![]()
例. 设一个种群分成3个年龄组,各年龄组的繁殖率为 b1=0,b2=5, b3=2,存活率为s1=0.8,s2=0.5.
确定各年龄组的收获系数以实现持续稳定收获.
求种群及收获量按年龄组的稳定分布.
持续稳定收获
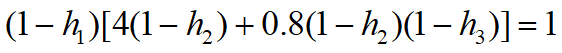
1. 取h1=0,
h2=0.75, h3=1
2. 取h1=0.5,h2=0.5, h3=1
1.不出售幼畜, 出售75%成年牲畜及全部老年牲畜.
2.出售50%的幼畜和成年牲畜及全部老年牲畜.
种群数量的稳定分布
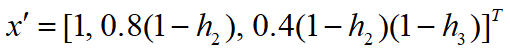
![]()
收获量的稳定分布
![]()
![]()
小结与评注:
模型基本假定:种群参数(繁殖率、存活率)只与年龄有关, 与时段无关(稳定环境、时间不长).
Leslie矩阵为常数矩阵L——可用特征根方法作稳定性分析.
如果种群参数随时段变化(L= L(k)), 模型表为
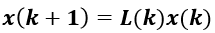 ,无稳定性分析.
,无稳定性分析.人口增长与动物种群数量变化规律相同, 类似建立离散型女性人口模型——Leslie模型.
扩展:中国人口增长预测(参加更多案例)