5.5  食饵-捕食者模型

背景和问题：

• 种群甲靠丰富的天然资源生存，种群乙靠捕食甲为生，形成食饵-捕食者系统(P-P系统），如食用鱼和鲨鱼，美洲兔和山猫，害虫和益虫.

• 模型的历史背景——一次世界大战期间地中海渔业的捕捞量下降(食用鱼和鲨鱼同时捕捞)，但是其中鲨鱼的比例却增加，为什么？

模型建立：食饵-捕食者模型(Volterra)

• 食饵(甲)数量 x(t), 捕食者(乙)数量 y(t)

  甲独立生存的增长率 r；乙使甲的增长率减小，减小量与 y成正比

      ，a～捕食者掠取食饵能力

  乙独立生存的死亡率 d；甲使乙的死亡率减小，减小量与 x成正比

      ，b～食饵供养捕食者能力

• 方程(1),(2)无解析解

模型分析：

1、用数学软件MATLAB求微分方程数值解

• 

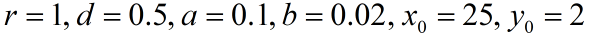
• 计算结果（数值，图形）Þ观察，猜测

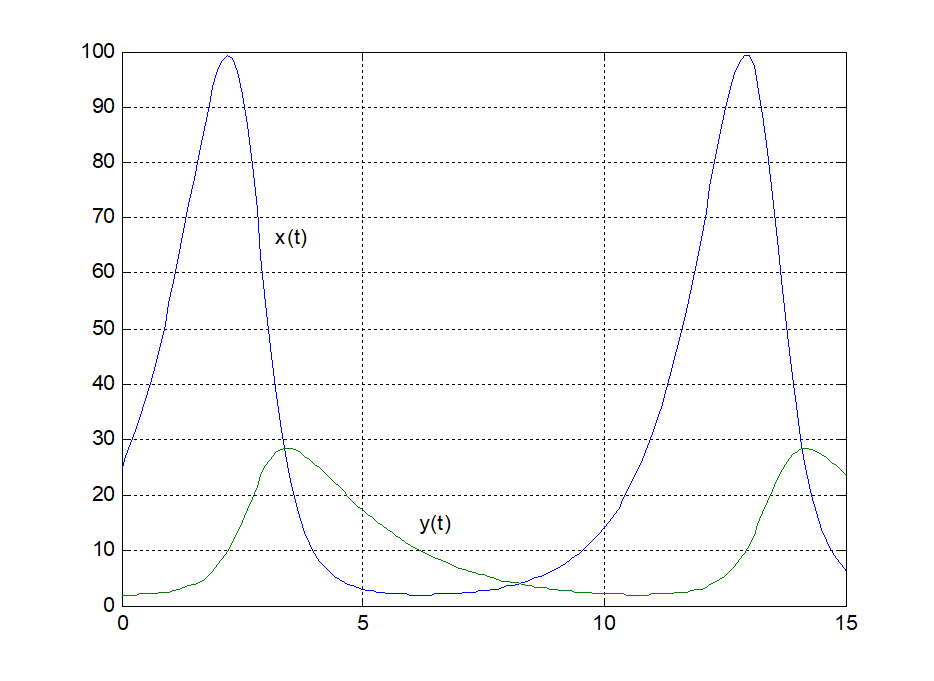
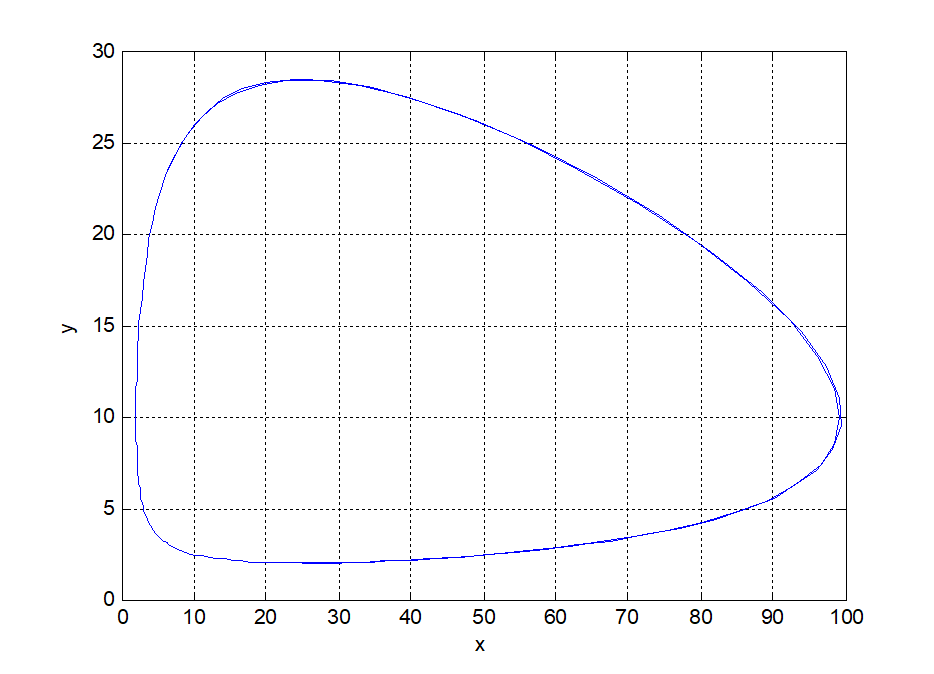
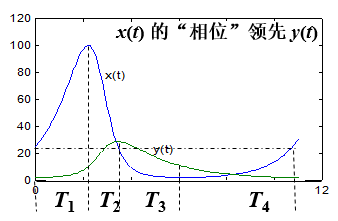
• x(t), y(t)是周期函数，相图(x,y)是封闭曲线；

• x(t), y(t)的周期约为10.7；

• xmax=99.3, xmin=2.0, ymax=28.4, ymin=2.0.

• 用数值积分可算出x(t), y(t)一周期的平均值

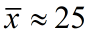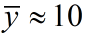  ， ～代表食饵和捕食者的平均密度

2、平衡点及相轨线

• Volterra模型的平衡点及其稳定性

  平衡点

  P点稳定性不能用近似线性方程分析（用微分方程稳定性理论分析失效）

• 用相轨线分析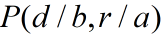点稳定性

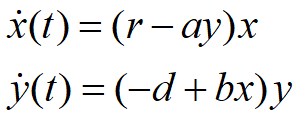  Þ

  相轨线

• 在相平面上讨论相轨线的图形：

  
  

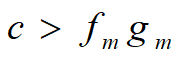  时无相轨线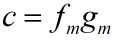

  相轨线退化为P点

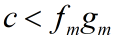  相轨线是一条封闭曲线族

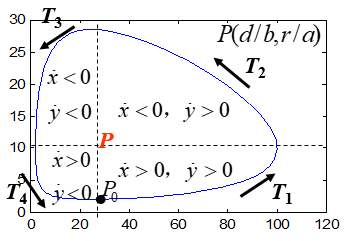
  当c由最大值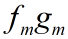变小时，相轨线是一族从中心P点向外扩展的封闭曲线（如图），P点称为中心。因而P点不是稳定的平衡点。

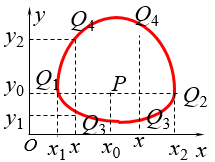
• 相轨线的方向：逆时针

3、x(t), y(t)在一个周期内的平均值

• 由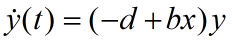Þ
  

        Þ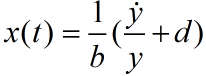

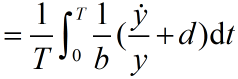
   由Þ.....Þ

  即x(t), y(t)在一个周期内的平均值正是相轨线中心P点的坐标。

模型解释：

• 捕食者数量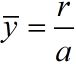，捕食者数量与食饵增长率r成正比,与捕食者掠取食饵能力a成反比。

  食饵数量，食饵数量与捕食者死亡率d成正比,与食饵供养捕食者能力b成反比。

• 一次大战期间地中海渔业的捕捞量下降，但是其中鲨鱼的比例却在增加，为什么？

  自然环境

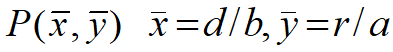
  捕捞Þ

  战时捕捞Þ

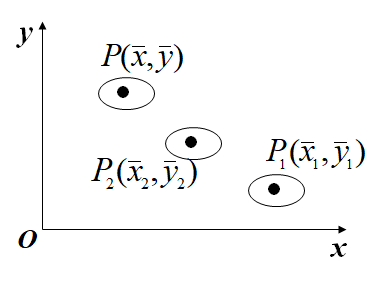
  食饵(鱼)减少，捕食者(鲨鱼)增加。

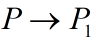• 还表明：对害虫(食饵)—益虫(捕食者)系统，使用灭两种虫的杀虫剂,会使害虫增加，益虫减少。

• 食饵-捕食者模型(Volterra)的局限性与改进。