7.2   公平的席位分配

背景：

• 每10年，美国联邦政府进行一次全国人口普查, 各州在联邦众议院的代表名额也据此重新确定.

• 2000年人口普查后，犹他州向联邦政府提出控诉，说分配给北卡罗莱纳州的名额应该是他们的.

• 事实上，过去200年来，美国国会在名额分配上打过多起法律官司，曾有过长期争论并使用过4种分配方案.

• 问题的数学本质是什么？——公平的席位分配问题（apportionment）

问题：一个简单例子

• 三个系学生共200名(甲100，乙60，丙40)，代表会议共20席，按比例分配，三个系分别为10, 6, 4席.

• 因学生转系, 三系人数为103, 63, 34, 如何分配20席?

• 若代表会议增加1席，如何分配21席?

比例加惯例：

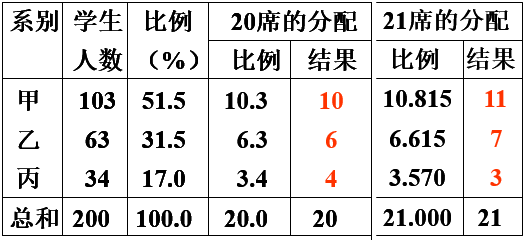
• 对丙系公平吗？

模型：

• 已知: m方人数分别为 p1, p2,…,pm, 记总人数为P =p1+p2+…+pm,  待分配的总席位为N. 记 qi  =Npi/P,  称为第i方的份额(i=1,2, …,m) 

要求：

• 已知份额向量q=(q1, …, qm)>0, 找一个非负整数分配向量n=(n1, …, nm), 使n与q最接近.

比例加惯例法：

• 各方先分配qi的整数部分[qi], 总余额为

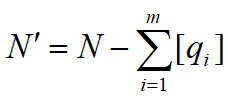
• 记ri=qi-[qi], 则第i方的分配名额ni为

背景：Hamilton(比例加惯例)方法：

• A. Hamilton提出的这种办法1792年被美国国会否决，

  1850-1900年被美国国会采用（称为Vinton法），

  又称为最大剩余法（GR: Greatest Remainders）或最大分数法（LF: Largest Fractions），等等

• 席位悖论—总席位增加反而可能导致某州席位减少，

  1880年Alabama州曾遇到，又称Alabama悖论  

• 该方法的另一个重大缺陷：（后面给例子） 

  人口悖论—某州人口增加较多反而可能该州席位减少 

Hamilton方法的不公平性：

1.  p1, p2,…,pm不变, N的增加会使某个ni减少.（上例）

2. N不变, pi 比pj的增长率大, 会使 ni减少nj增加.（下例）

“公平”分配方法： 

• 衡量公平分配的数量指标

  当 p1/n1=p2/n2时，分配公平；若 p1/n1>p2/n2，对A不公平；

       p1/n1–p2/n2 ~ 对A的绝对不公平度。

•  p1=150,  n1=10,  p1/n1=15；p2=100,  n2=10,  p2/n2=10

       p1=1050,  n1=10, p1/n1=105；p2=1000,  n2=10,  p2/n2=100

  虽二者的绝对不公平度相同，但后者对A的不公平程度已大大降低!

• 将绝对度量改为相对度量：

  若 p1/n1>p2/n2，定义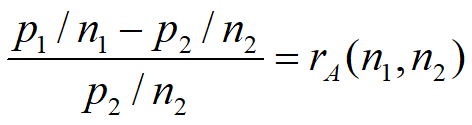

       ~ 对A的相对不公平度。类似地定义 rB(n1,n2)

• 公平分配方案应使rA , rB尽量小

• 将一次性的席位分配转化为动态的席位分配, 即
  

  设A, B已分别有n1,n2席, 若增加1席, 问应分给A, 还是B?

• 不妨设分配开始时p1/n1>p2/n2，即对A不公平.

• 讨论以下几种情况：设初始p1/n1>p2/n2 

  1）若p1/(n1+1)>p2/n2，则这席应给 A

  2）若p1/(n1+1)<p2/n2，应计算rB(n1+1, n2)

  3）若p1/n1>p2/(n2+1)，应计算rA(n1,n2+1)

• 问：p1/n1<p2/(n2+1)  是否会出现？否!

  若rB(n1+1,n2) < rA(n1,n2+1),  则这席应给A

• 若rB(n1+1,n2) >rA(n1,n2+1),  则这席应给B

• 当rB(n1+1,n2) < rA(n1,n2+1),  该席给A，由rA, rB的定义得

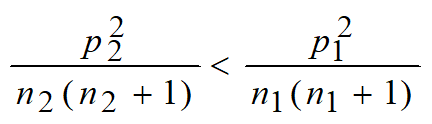
  该席给A，否则，该席给B

• 定义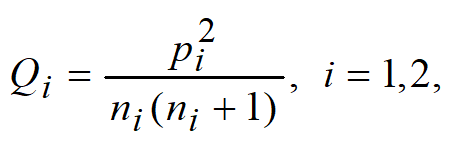该席给Q值较大的一方。

• 推广到m方分配席位：

  计算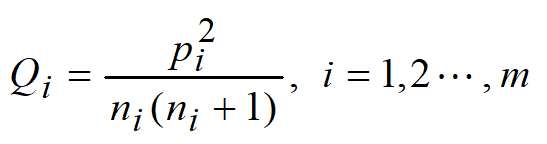，该席给Q值最大的一方！

        ——称为Q值法  相等比例法, 即EP法(Huntington, 1921)

• 三系用Q值法重新分配21个席位：

  一席一席地将前19席分配完毕后的结果

  甲系：p1=103,n1=10；乙系：p2=  63, n2=  6；丙系：p3=  34, n3=  3

   ——与Hamilton法结果相同

  第20席： ，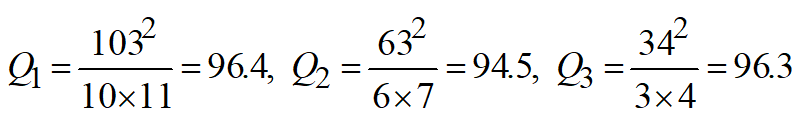

       Q1最大，第20席给甲系

  第21席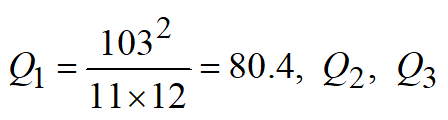：同上，Q3最大，第21席给丙系

• Q 值法分配结果：甲系11席, 乙系6席, 丙系4席——公平吗？

• Q 值方法是20世纪20年代由哈佛大学数学家E.V.Huntington提出和推荐的一系列席位分配方法中的一个。

• 除数法（Huntington，1921）

• EP法每增加1席地计算，不会出现席位悖论和人口悖论.

• 有没有其他的不公平度衡量指标？

• 20世纪20年代哈佛大学E.V. Huntington 做了系统研究.

• 对于非负整数n定义一个非负单调增函数d(n)

• 当总席位为s时第i方分配的席位记作fi(p, s), fi(p, 0)=0

• 让s每次1席地递增至N，按照以下准则分配:

• 记ni=fi(p, s)，若

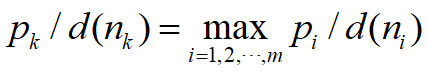
  则令fk(p, s+1)= nk+1, fi(p, s+1) = ni (i≠k)

５种除数法：

  最大除数法（GD：Greatestdivisors)

  主要分数法（MF：Majorfraction)

  相等比例法（EP：Equalproportions)

  调和平均法（HM：Harmonicmean)

  最小除数法（SD：Smallestdivisors)

• 模型的公理化研究

  EP方法比最大剩余法(GR)更公平吗？

•  已知总席位数s,人口向量p=(p1, p2,…,pm), P=Σpi

• 份额向量q = (q1, …, qm)， qi=spi/P 

• ni＝fi(p,s)表示人数为p、总席位为s时分配给第i方席位

• 关键性质

  1) 　~份额性

  2) fi (p,s)£ fi (p,s+1)  ~ 席位单调性

  3) 若pi' /pj'  ≥ pi/pj, 则fi(p', s) ≥ fi(p, s), 或fj(p', s) £  fj(p, s) ~人口单调性

• GR方法满足性质1，但不满足性质2, 3. 除数方法满足性质2, 3, 但不满足性质1 .
  

• 已经证明：对于m≥4,N≥m+3, 不存在满足3条性质(份额性、席位单调性、人口单调性) 的分配方法.

• 可以找到同时满足份额性和席位单调性的方法.