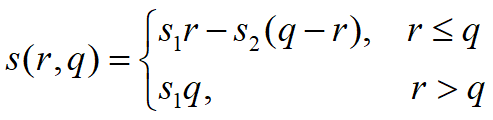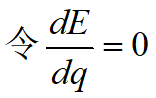8 概率模型
现实世界的变化受着众多因素的影响:确定性因素和随机性因素
确定性模型:随机因素可以忽略;随机因素影响可以简单地以平均值的作用出现
随机性模型:随机因素对研究对象的影响必须考虑
本章讨论,如何用随机变量和概率分布描述随机因素的影响,建立比较简单的随机模型——概率模型,期中要用到概率的运算,以及概率分布、期望、方差等基本知识。
8.1 报童的诀窍
背景和问题:
报童售报:4元 (零售价)>2元(购进价)>1元(退回价)
售出一份赚2元;退回一份赔1元
每天购进多少份报纸可使收入最大?
问题分析:
购进太多®卖不完退回®赔钱;购进太少®不够销售®赚钱少;
应根据需求确定购进量
存在一个合适的购进量
每天需求量是随机的
每天收入是随机的
优化问题的目标函数应是长期的日平均收入,等于每天收入的期望
离散型需求下的报童售报模型
问题
将需求量看作离散型随机变量,100份为1单位
由统计资料得到需求量概率分布如下表

建模
记需求量为r 时的概率为f(r), r=0,1,2…,n
已知售出1单位获利s1;退回1单位损失s2
设报童每天购进q单位报纸,每天需求量为r
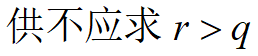
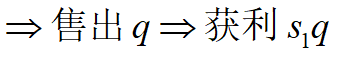
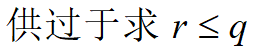
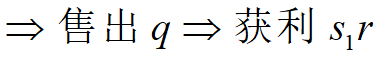
![]()
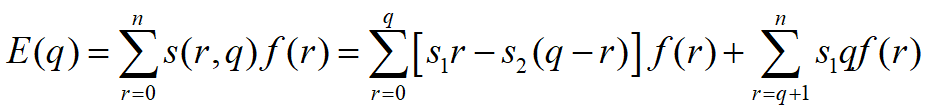
![]()
![]()
求解
![]()
![]()
![]()
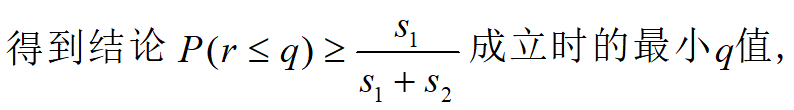
![]()
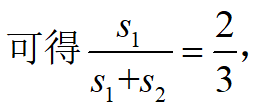
![]()
![]()
![]()
![]()
![]()
分析
 ~符合常识
~符合常识
连续型需求下的报童售报模型
问题
将需求量视为连续型随机变量,以1份为1单位
用概率密度描述概率分布,更为方便
设由统计资料和经验判断, 需求量大致服从正态分布
设其平均值是260, 标准差是50, 即需求量为N(260,502)
报童仍然1份报纸2元买进,4元售出,退回得到1元补偿
即售出1份获利2元; 因剩余而退回1份损失1元
问报童每天应该购进多少份报纸, 才能获得最高的日均利润?
建模
记需求量的概率密度为p(r),
已知售出1单位获利s1;退回1单位损失s2
设报童每天购进q单位报纸
![]()
![]()
求解
![]()
![]()
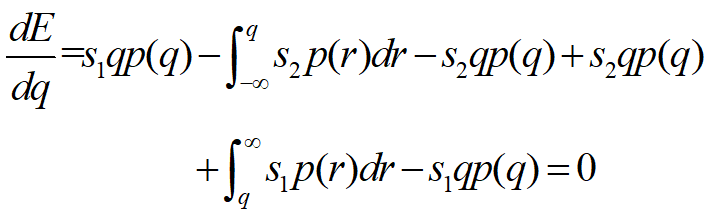
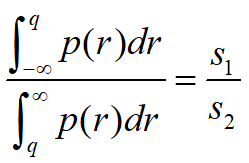 ,简化为
,简化为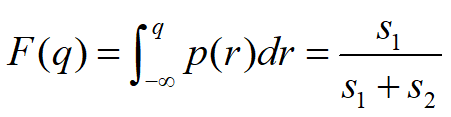
结果与离散模型一致

需求量概率分布为N(260,502)
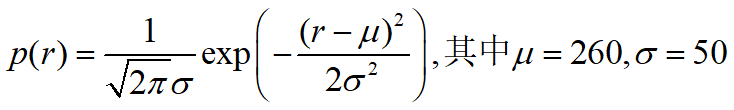
![]()
利用MATLAB软件,q=norminv(p,mu, sigma)
计算得q=282
报童每天购进282份报纸能获得最高的日均利润
将q=282代入公式计算可得最高日均利润E(q)的数值
分析
可以用概率密度p(r)的图形直观表示
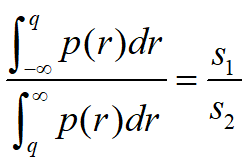
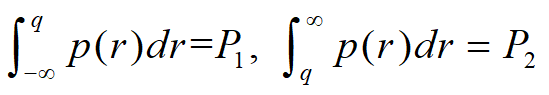
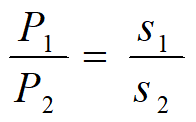
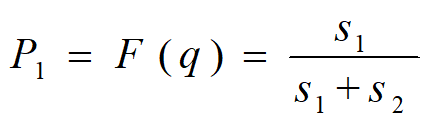
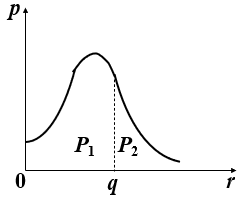
s1~售出一份赚的钱, s2~退回一份赔的钱
![]()