9  统计模型

• 由于客观事物内部规律的复杂及人们认识程度的限制，无法分析实际对象内在的因果关系，建立合乎机理规律的数学模型.  

• 通常的办法是搜集大量的数据，通过对数据的统计分析，找出与数据拟合最好的模型.

• 回归模型是用统计分析方法建立的最常用的一类模型.

• 不涉及回归分析的数学原理和方法 .
  

• 通过实例讨论如何选择不同类型的模型 .

• 对软件得到的结果进行分析，对模型进行改进.

   

9.1  牙膏的销售量

背景和问题：

• 建立牙膏销售量与价格、广告投入之间的模型;

• 预测在不同价格和广告费用下的牙膏销售量. 

• 收集了30个销售周期本公司牙膏销售量、价格、广告费用，及同期其他厂家同类牙膏的平均售价.（数据参见教材）

模型建立和求解：

• 先作散点图观察

（1）基本模型：

模型1：

  其中为价格差，为广告费，为随机误差，服从均值为零的正态分布。

模型求解：

• 由数据 y, x1,x2估计b

• MATLAB 统计工具箱函数调用格式：

 [b,bint,r,rint,stats]=regress(Y,X,alpha)

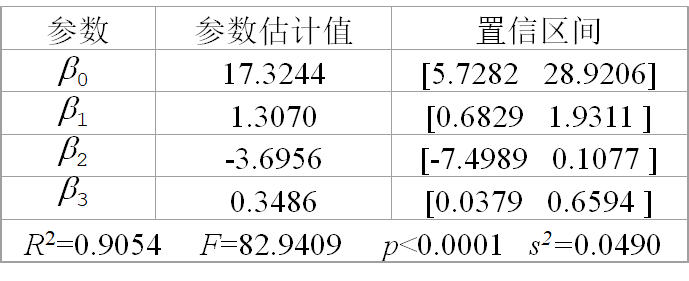
结果分析：

• y的90.54%可由模型确定；F值远超过F检验的临界值；p值远小于a=0.05，模型从整体上看成立

• b2的置信区间包含零点(右端点距零点很近) ，x2对因变量y 的影响不太显著

• x22项显著，可将x2保留在模型中 

• 销售量预测：

  

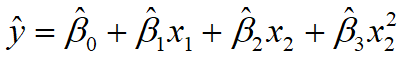
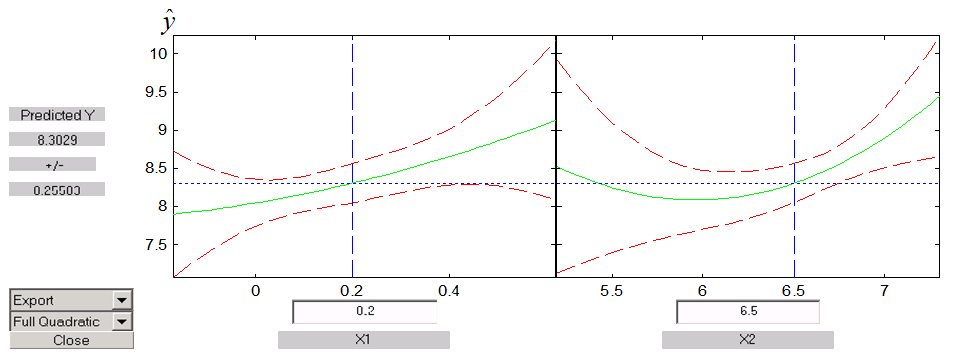
控制价格差 x1=0.2元，投入广告费x2=6.5百万元

(百万支)

销售量预测区间为 [7.8230，8.7636]（置信度95%）

• 模型改进：考虑x1和x2对y的影响有交互作用

模型2：

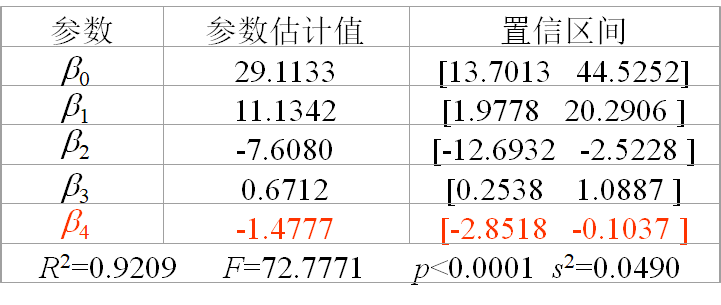
预测值，预测区间 [7.8953，8.7592] 

(3) 完全二次多项式回归模型

模型3：

调用函数RSTOOL以交互式画面给出值及其预测区间。

调用格式为 RSTOOL（X,Y,'model')

其中X为自变量的数据构成的结构矩阵，Y为因变量的数据，model为模型选项，这里选'quddratic'表示全二次多项式。