8.2  钢琴销售的存贮策略 

马氏链模型

• 马氏链（Markov Chain）是随机过程的一个特例，专门研究无后效条件下时间和状态均为离散的随机转移问题，但在建模过程中采用线性代数的方法，因此，也在线性代数模型中来学习。

• 马氏链模型在经济、社会、生态、遗传等许多领域中有着广泛的应用，值得提出的是，虽然它是解决随机转移过程的工具，但是在一些确定性系统的状态转移问题也能用马氏链模型处理。

钢琴销售的存贮策略

背景和问题：

• 钢琴销售量很小，商店的库存量不大以免积压资金 

• 一家商店根据经验估计，平均每周的钢琴需求为1架

• 存贮策略：每周末检查库存量，仅当库存量为零时，才订购3架供下周销售；否则，不订购。 

• 估计在这种策略下失去销售机会的可能性有多大，以及每周的平均销售量是多少。 

问题分析：

• 顾客的到来相互独立，需求量近似服从泊松分布，其参数由需求均值为每周1架确定，由此计算需求概率。 

• 存贮策略是周末库存量为零时订购3架周，末的库存量可能是0, 1, 2, 3，周初的库存量可能是1, 2, 3。

• 用马氏链描述不同需求导致的周初库存状态的变化。

• 动态过程中每周销售量不同，失去销售机会（需求超过库存）的概率不同。 

• 可按稳态情况（时间充分长以后）计算失去销售机会的概率和每周的平均销售量。 

模型假设： 

1. 钢琴每周需求量服从泊松分布，均值为每周1架。 

2. 存贮策略：当周末库存量为零时，订购3架，周初到货；否则，不订购。 

3. 以每周初的库存量作为状态变量，状态转移具有无后效性。 

4. 在稳态情况下计算该存贮策略失去销售机会的概率，和每周的平均销售量。 

模型建立：

Dn~第n周需求量，均值为1的泊松分布 

Sn~第n周初库存量(状态变量 )

状态转移规律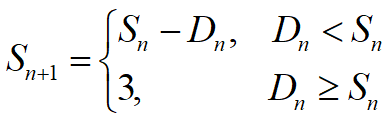 

状态转移阵 

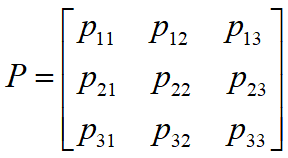
状态概率 

马氏链的基本方程

已知初始状态，可预测第n周初库存量Sn= i 的概率

n®¥, 状态概率

模型求解：

1. 估计在这种策略下失去销售机会的可能性

第n周失去销售机会的概率 

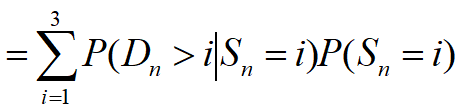
• 从长期看，失去销售机会的可能性大约 10%。

2. 估计这种策略下每周的平均销售量

第n周平均售量

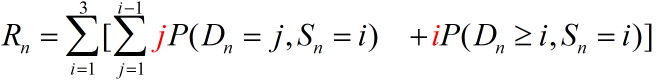
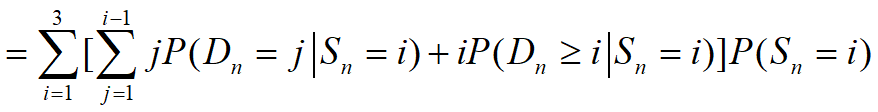
• 从长期看，每周的平均销售量为 0.857(架) 

敏感性分析：

• 当平均需求在每周1 (架) 附近波动时，最终结果有多大变化。