1.3  建模示例之一 包饺子中的数学

背景和问题：

通常，1kg馅，1kg面，包100个饺子. 今天，馅比1kg多，1kg面不变，要把馅包完. 应多包几个（每个小些），还是少包几个（每个大些）？若回答是包大饺子，那么若100个饺子包1kg馅，问50个饺子能包多少馅？

问题分析：

• 直观认识：“大饺子包的馅多”！但是：“用的面皮也多”！

• 需要比较：饺子从小变大时馅和面增加的数量关系.

• 建立馅、皮与数学概念的联系：馅——体积，皮——表面积

• 体积V、面积S的一个大饺子 → 体积v、面积s的n个小饺子 

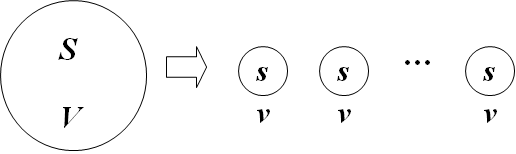
  V和nv哪个大？  定性分析

  V比nv大多少？  定量分析

模型假设：

     1. 皮的厚度一样 → S=ns  （1）

  2. 饺子的形状一样 → 两个k1（及k2）一样

模型建立：

• 体积与面积的联系——半径（特征半径）

  R～大皮半径  ,  →   (2)

  r～小皮半径  ,  →   (3)

  由(1),(2),(3)，可推出 

结果解释：

定性分析： V比nv大（n>1）——大饺子包的馅多

定量分析：V是nv的 倍

模型应用：

• 若100个饺子包1kg馅，50个饺子能包多少馅？

  50个饺子能包1.4kg馅.

讨论：

• 日常生活中有哪些可用这个模型解释的现象？