3.4 易拉罐形状和尺寸的最优设计
全国大学生数学建模竞赛2006年C题
以发表在《工程数学学报》2006年增刊上学生优秀论文和评述文章为基本材料, 介绍建模过程。
赛题原文
我们只要稍加留意就会发现销量很大的饮料 (例如饮料量为355毫升的可口可乐、青岛啤酒等)的饮料罐(即易拉罐)的形状和尺寸几乎都是一样的。看来，这并非偶然，这应该是某种意义下的最优设计。当然，对于单个的易拉罐来说，这种最优设计可以节省的钱可能是很有限的，但是如果是生产几亿，甚至几十亿个易拉罐的话，可以节约的钱就很可观了。
现在就请你们小组来研究易拉罐的形状和尺寸的最优设计问题。具体说，请你们完成以下的任务：
1.取一个饮料量为355毫升的易拉罐，例如355毫升的可口可乐饮料罐，测量你们认为验证模型所需要的数据，例如易拉罐各部分的直径、高度、厚度等，并把数据列表加以说明；如果数据不是你们自己测量得到的，那么你们必须注明出处。
2.设易拉罐是一个正圆柱体, 什么是它的最优设计？其结果是否可以合理地说明你们所测量的易拉罐的形状和尺寸，例如说，半径和高之比，等等。
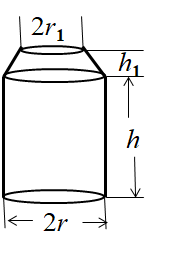
3.设易拉罐的中心纵断面如图所示, 上面部分是一个正圆台,下面部分是一个正圆柱体.什么是它的最优设计？其结果是否可以合理地说明你们所测量的易拉罐的形状和尺寸。
4.利用你们对所测量的易拉罐的洞察和想象力,做出你们自己的关于易拉罐形状和尺寸的最优设计。
5.用你们做本题及以前学习和实践数学建模的亲身体验,写一篇短文(不超过1000字,你们的论文中必须包括这篇短文),阐述什么是数学建模, 它的关键步骤及难点。
问题分析——导数应用中的极值问题
设计一个容积固定、有盖的圆柱形容器, 若侧壁及底、盖厚度都相同, 问容器高度与底面半径之比为多少, 所耗材料最少？
侧壁及底、盖厚度相同，所耗材料用总面积表示
r
底面半径. h
，
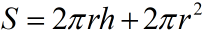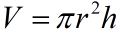，V固定, 求r，h满足什么关系使S最小。
微分法求解
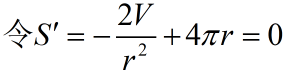
容器高度与底面直径相等时所耗材料最少。
思考：
1.通常易拉罐的高度比底面直径大得多？
2.如果只考虑节省材料：
罐底、盖厚度比侧壁大 Þ 增加高度、减少底面直径
题目要求测量数据 Þ 得到底、盖、侧壁的厚度
正圆柱体利用简单几何知识建模。
3.圆柱体上面有一个小圆台 Þ 小圆台改为小球台
数据测量
易拉罐各项尺寸(mm)，从罐的外部进行测量，5只罐子的平均值：
圆台高不到圆柱高的10%，顶盖与圆柱直径相差10% Þ 圆台近似作圆柱处理误差很小。
罐底、盖的厚度约为罐壁的3倍 Þ 优化设计与普通的极值问题有别。
罐高约为圆柱直径的2倍，与日常所见相符。
圆柱模型
小圆台近似于圆柱，直径相同
所耗材料的体积=侧壁、底、盖面积×厚度
r
， 
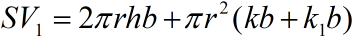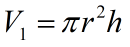，b, k,k1已知V1固定, 求r, h满足什么关系使SV1最小.
极值问题微分法求解：
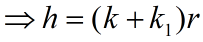
测量数据——底、盖厚度约为罐壁的3倍。
h=6r，圆柱高度为直径的3倍 Þ与测量数据和日常所见不符。
厚度测量存在较大误差；实际加工制作存在节省材料之外的其他原因。
圆台模型
顶部小圆台下面与圆柱相接
b
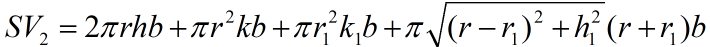
，b, k,k1已知
V2固定, 求r, h, r1, h1满足什么关系使SV2最小。
约束极小问题的数值解：
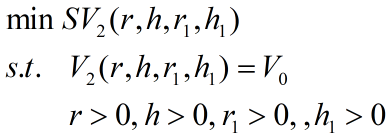，b,k,k1,V0已知
LINGO软件编程计算
r=31.43，h=108.34, r1=0,h1=28.10 (mm)圆台退化为圆锥。
结果分析：
假定圆台侧壁厚度=b, 罐盖厚度k1b =3b.
为节省材料需尽量减少罐盖面积 Þ r1=0
改进：
罐盖要安装拉环及工艺、美观等因素。
半径r1应有下限（设r1
20）
求解得 r=31.62, h=104.52, r1=20, h1=17.29(mm)
球台模型
顶部小圆台改为球台
b
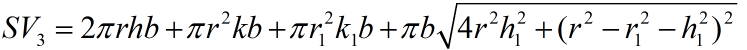
V3固定, 求r, h, r1, h1满足什么关系使SV3最小。
对半径r1加以限制, 求数值解。
小结与评注
从日常生活中发现与数学课本类似问题的结果有不同之处,在实践(测量数据)基础上给以分析和解决,有利于培养数学建模的意识和能力。
建模经过了从圆柱到圆台和球台、从材料厚度相同到不同、从解析解到数值解的过程,对于学习数学建模方法有启示和指导意义。
