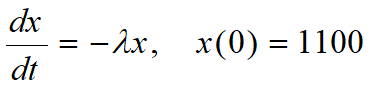5.2  药物中毒急救

背景和问题：

• 一天夜晚，你作为见习医生正在医院内科急诊室值班，两位家长带着一个孩子急匆匆进来，诉说两小时前孩子一口气误吞下11片治疗哮喘病的、剂量为每片100mg的氨茶碱片，已经出现呕吐、头晕等不良症状。

• 按照药品使用说明书，氨茶碱的每次用量成人是100～200mg，儿童是3～5mg/kg.

• 如果过量服用，可使血药浓度（单位血液容积中的药量）过高，当血药浓度达到100μg/ml时，会出现严重中毒，达到200μg/ml则可致命。

• 作为一名医生你清楚地知道，由于孩子服药是在两小时前，现在药物已经从胃进入肠道，无法再用刺激呕吐的办法排除。当前需要作出判断的是，孩子的血药浓度会不会达到100μg/ml甚至200μg/ml，如果会达到，则临床上应采取怎样的紧急施救方案?

调查与分析：

• 认为血液系统内药物的分布，即血药浓度是均匀的，可以将血液系统看作一个房室，建立“一室模型”.

• 血液系统对药物的吸收率(胃肠道到血液系统的转移率) 和排除率可以由半衰期确定.

• 半衰期可以从药品说明书上查到. 

• 血药浓度=药量/血液总量 

• 通常，血液总量约为人体体重的7~8%，体重50~60 kg的成年人有4000ml左右的血液. 

• 目测这个孩子的体重约为成年人的一半，可认为其血液总量约为2000ml. 

临床施救的办法：

• 口服活性炭来吸附药物，可使药物的排除率增加到原来（人体自身）的2倍. 
  

• 体外血液透析，药物排除率可增加到原来的6倍，但是安全性不能得到充分保证.

模型假设： 

记胃肠道中药量x(t),血液系统中药量y(t)，时间t以孩子误服药的时刻为起点（t=0）. 

1. 胃肠道中药物向血液的转移率与x(t)成正比，比例系数λ(>0)，总剂量1100mg药物在t=0瞬间进入胃肠道.

2. 血液系统中药物的排除率与y(t)成正比，比例系数μ(>0)，t=0时血液中无药物.

3. 氨茶碱被吸收的半衰期为5小时，排除的半衰期为6小时. 

4. 孩子的血液总量为2000ml. 

模型建立：

• x(t)下降速度与x(t)成正比（比例系数λ），总剂量1100mg药物在t=0瞬间进入胃肠道.

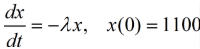
• y(t)由吸收而增长的速度是λx，由排除而减少的速度与y(t)成正比（比例系数μ） , t=0时血液中无药物.

模型求解： 

• ，

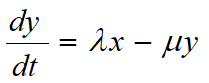
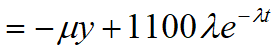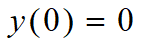
• 药物吸收的半衰期为5小时

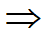
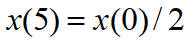
• 药物排除的半衰期为6小时，只考虑血液对药物的排除

         ，

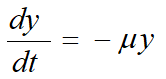结果及分析： 

• 胃肠道药量

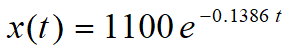
• 血液系统药量

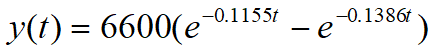
• 血液总量2000ml

  血药浓度100μg/ml Û y(t) =200mg Þ 严重中毒

  血药浓度200μg/ml Û y(t) =400mg Þ 致命

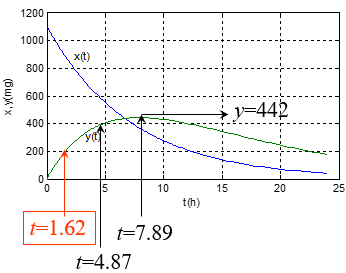
• y(2)=236.5 ，孩子到达医院前已严重中毒，如不及时施救，约3小时后将致命！

施救方案： 

• 口服活性炭使药物排除率μ增至原来的2倍.

• 孩子到达医院(t=2)就开始施救，血液中药量记作z(t) 

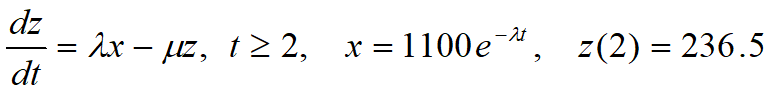
       λ=0.1386 (不变)，μ=0.1155*2=0.2310 

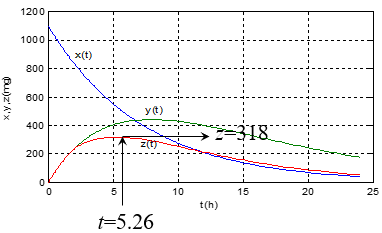
• 施救后血液中药量z(t)显著低于y(t). 

• z(t)最大值低于致命水平.

• 要使z(t)在施救后立即下降，可算出μ至少应为0.4885. 

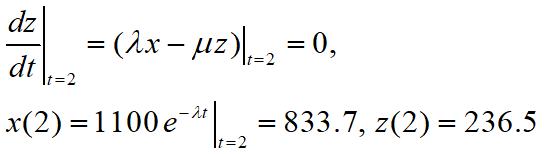
• 若采用体外血液透析，μ可增至0.1155*6=0.693，血液中药量下降更快；临床上是否需要采取这种办法，当由医生综合考虑并征求病人家属意见后确定. 

小结与评注:

• 以药物中毒急救为背景，研究药物通过胃肠道向血液系统的转移，以及从血液系统的排除.

• “ 转移率和排除率与血药浓度成正比”是药物动力学建立房室模型的基本假设.

• 假定整个血液系统的血药浓度均匀（用一个时间函数表示），建立最简单的一室模型，用一阶微分方程即可求解.