5.4 捕鱼业的持续收获
背景
可再生资源(渔业、林业等)与非可再生资源(矿业等).
可再生资源应适度开发——在持续稳产前提下实现最大产量或最佳效益.
问题及分析
如果使捕捞量等于自然增长量,渔场鱼量将保持不变,则捕捞量稳定.
1.建立捕捞情况下渔场鱼量遵从的方程,分析鱼量稳定的条件.
2.在鱼量稳定的条件下,如何控制捕捞使持续产量最大或经济效益最佳? 捕捞过渡?
产量模型 设x(t)~渔场鱼量
假设
无捕捞时鱼的自然增长服从Logistic规律. r~固有增长率, N~最大鱼量
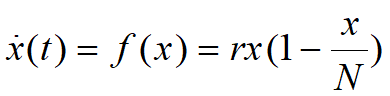
单位时间捕捞量与渔场鱼量成正比.
h(x)= Ex, E~捕捞强度
建模
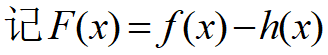 ,有捕捞情况下渔场鱼量满足
,有捕捞情况下渔场鱼量满足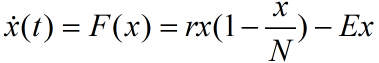
不需要求解x(t),只需知道x(t)稳定的条件.
一阶微分方程的平衡点及其稳定性
产量模型
令
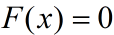 ,平衡点
,平衡点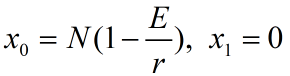
稳定性判断
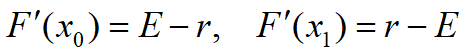
当
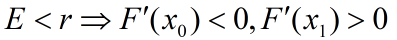 Þ
Þ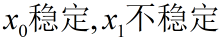
当
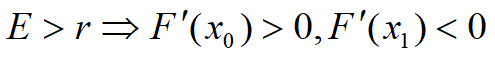 Þ
Þ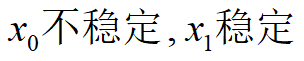
E~捕捞强度,r~固有增长率
x0稳定,可得到稳定产量;x1稳定,渔场干枯
分析表明:只要捕捞适度(
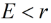 ),就可使渔场鱼量稳定在x0,从而获得持续产量 h(x0)=Ex0.
),就可使渔场鱼量稳定在x0,从而获得持续产量 h(x0)=Ex0.进一步讨论,在鱼量稳定在x0的条件下,如何控制捕捞强度E使持续产量最大?
图解法
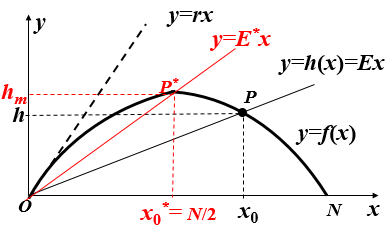
P的横坐标x0~平衡点,P的纵坐标h~产量
产量最大
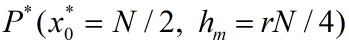 ,
,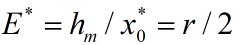
结论
捕捞率控制在固有增长率r的一半,或者控制渔场鱼量为最大鱼量N的一半时,获得最大产量.
效益模型
在鱼量稳定在x0的条件下,如何控制捕捞强度E使效益最大?
假设
鱼销售价格p,单位捕捞强度费用c
收入 T =ph(x)= pEx,支出 S =cE
单位时间利润
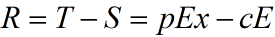 ,
,以稳定平衡点
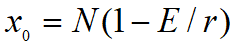 代入得
代入得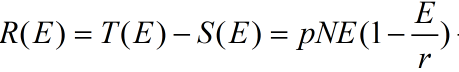
求E使R(E)最大 Þ
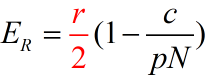
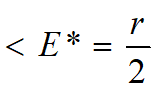
最大利润下渔场稳定鱼量
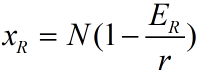
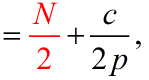
单位时间的持续产量
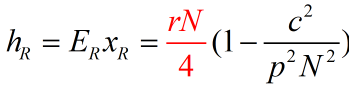
捕捞过度
封闭式捕捞追求利润R(E)最大,此时
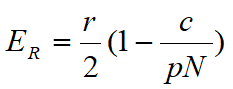
开放式捕捞只求利润R(E)>0
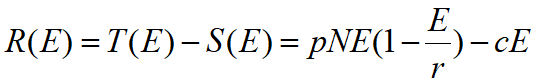
令=0,
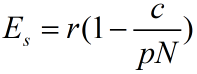
R(E)=0时的捕捞强度Es= 2ER ~临界强度
临界强度下的渔场鱼量
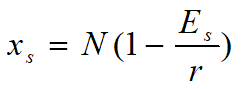
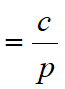
xs由成本—价格比决定
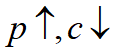 Þ
Þ 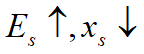
捕捞过度~图解法
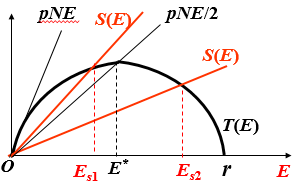
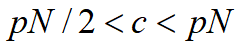
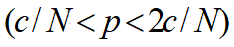
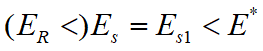 ~经济学捕捞过度
~经济学捕捞过度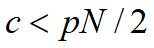
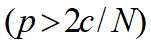
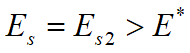 ~生态学捕捞过度
~生态学捕捞过度
小结
在自然增长和捕捞情况的合理假设下建模.
用平衡点稳定性分析确定渔场鱼量稳定条件,讨论产量、效益和捕捞过度3个模型.
课后扩展阅读:


