7 离散模型
离散模型:代数方程与差分方程(第6章)、整数规划(第4章)、图论、对策论、网络流、…
应用较广,是分析社会经济系统的有力工具.
只用到代数、集合及(少许)图论的知识.
7.1 职员晋升
日常工作、生活中的决策问题.
涉及经济、社会等方面的因素.
作比较判断时人的主观选择起相当大的作用,各因素的重要性难以量化.
Saaty于20世纪70年代提出层次分析法AHP (Analytic Hierarchy Process).
AHP——一种定性与定量相结合的、系统化、层次化的分析方法.
职员晋升
职场中如何公平、公正地实施职员晋升?管理者的一种简单易行、具有一定合理性的决策办法.
订立全面评价一位职员的几条准则,如工作年限、教育程度、工作能力、道德品质等;
确定各条准则在目标(职员晋升)中所占的权重;
按照每一准则对各位申报者进行比较和评判;
将准则的权重与按准则评判的结果加以综合,得到各位申报者的排序,作为职员晋升的决策.
层次分析法将定性分析与定量分析结合起来完成以上步骤,给出决策问题的定量结果.
层次分析法(AHP)的几个要素
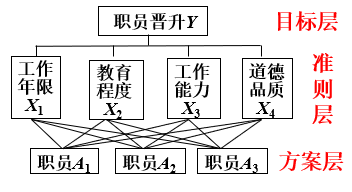
1. 层次结构图
将决策问题自上而下地分为目标、准则、方案3个层次,直观地用一个层次结构图表示.
确定各准则对目标的权重.
确定各方案对每一准则的权重.
二者综合得到方案对目标的权重.
2. 成对比较矩阵和特征向量
确定n个准则X1,X2,… X4对目标Y的权重.
n个准则两两对比: aij~ Xi和Xj对Y的重要性之比
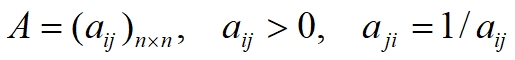 , A~成对比较阵,正互反阵
, A~成对比较阵,正互反阵对比采用相对尺度
工作年限X1,教育程度X2,工作能力X3,道德品质X4对职员晋升Y的成对比较阵:
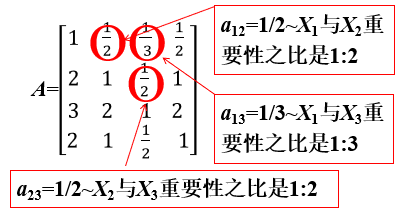
成对比较的一致性
a12=1/2 ~X1与X2重要性之比是1:2
a23=1/2 ~X2与X3重要性之比是1:2
由成对比较一致性,可推得,X1与X3重要性之比应是1:4
而a13=1/3 ~成对比较不一致
n个元素需做n(n-1)/2次成对比较, 要求全部一致是不现实、也不必要的.
AHP容许成对比较存在不一致,并确定了这种不一致的容许范围.
成对比较完全一致
假定X1,X2,…,Xn对Y的重要性之比已精确测定为w1:w2…:wn
设
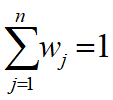 ,令aij=wi/wj
,令aij=wi/wj
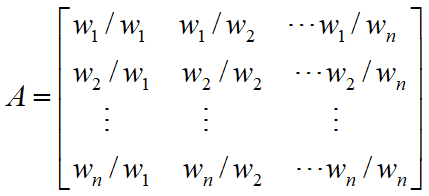
成对比较阵A满足
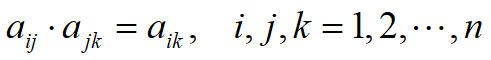 称为一致阵.
称为一致阵. 一致阵的各列均相差一个比例因子
一致阵A的代数性质:秩为1, 唯一非零特征根为n.
任一列向量都是对应于n的特征向量.
取权向量为w=(w1,w2,...,wn)T ,
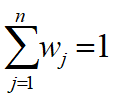
如果成对比较阵A不一致(但在容许范围内),
用对应于A最大特征根λ的特征向量(归一化后)为权向量w
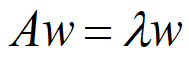
3. 一致性指标和一致性检验
界定成对比较阵 (正互反阵) A不一致的范围.
n阶正互反阵A的最大特征根λ ≥ n, A是一致阵的充要条件为λ= n.
λ比n大得越多, A与一致阵相差越大, 用特征向量作为权向量引起的判断误差越大.
用λ-n的大小衡量A的不一致程度.
Saaty定义一致性指标:
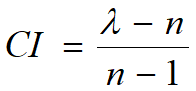
CI=0时A是一致阵, CI越大A越不一致.
制定衡量CI数值的标准,界定A不一致的范围.
Saaty引入随机一致性指标RI——从1,2,…,9及1,1/2,…,1/9随机取值构成A, 计算CI的平均值作为RI.
Saaty给出

应用时将n阶成对比较阵A的CI与同阶的RI比较.
定义一致性比率CR = CI/RI
当CR<0.1时通过一致性检验.
“职员晋升”中准则层对目标的权向量及一致性检验:
准则对目标的成对比较阵
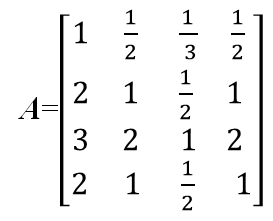
计算最大特征根λ、特征向量w及一致性指标CI.
λ=4.0104
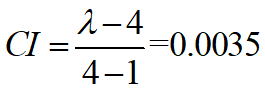 , RI=0.90
, RI=0.90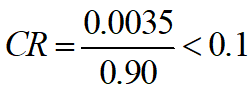
一致性检验通过
归一化的w=(0.1223,0.2270,0.4236,0.2270)T为权向量.
4. 综合权重
3位职员对4个准则的成对比较阵
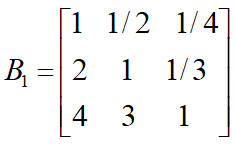
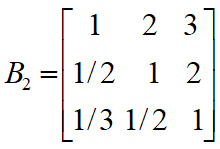
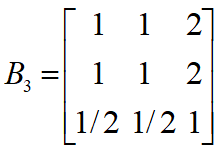
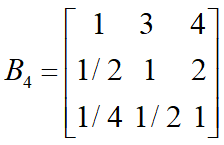
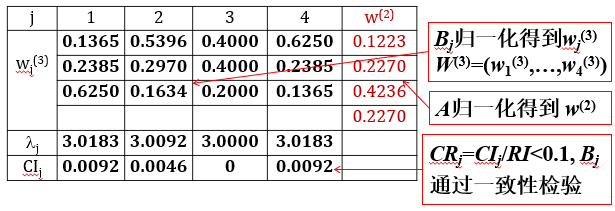
3位职员对晋升的综合权重
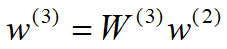 =(0.4505, 0.3202, 0.2292)T
=(0.4505, 0.3202, 0.2292)T3位职员的优劣顺序为A1, A2,A3
W(3)~第3层(方案)对第2层(准则)的权向量构成的矩阵
w(2)~第2层(准则)对第1层(目标)的权向量
w(3)~第3层(方案)对第1层(目标)的权向量
AHP推广到s层

分层加权和法
W(k)~第k层对第k-1层的权向量构成的矩阵
w(s)~最下层对第1层的权向量
5. 1-9比较尺度
Saaty提出1~9尺度: aij=1,2,…,9及1,1/2,,…,1/9.
便于定性到定量的转化:
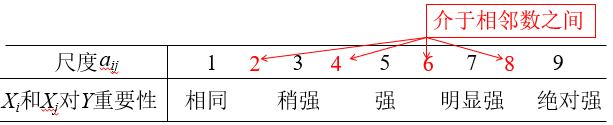
aij = 1,1/2,,…,1/9 ~Xi和Xj对Y重要性与上面相反
心理学家认为成对比较的因素不宜超过9个.用1~3,1~5,…,1~17,…,
1p~9p(p=2,3,4,5), d+0.1~d+0.9 (d=1,2,3,4)等27种比较尺度对若干实例构造成对比较阵,算出权向量,与实际对比发现, 1~9尺度较优.
职员晋升问题的再讨论
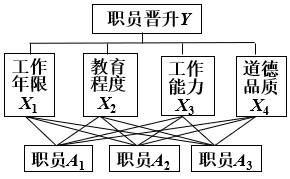
每一准则分若干等级:工作年限、教育程度用入职时间和学历分级, 工作能力、道德品质按照优、良、中划分.
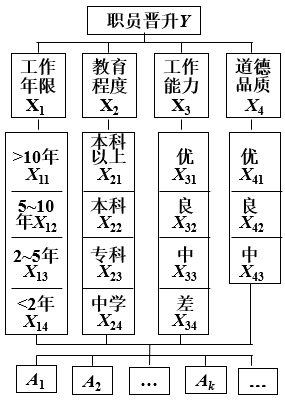
4个准则的权重仍为成对比较得到的w1,w2,w3,w4.
每一准则中最高等级为100分,决定其他分数wij.
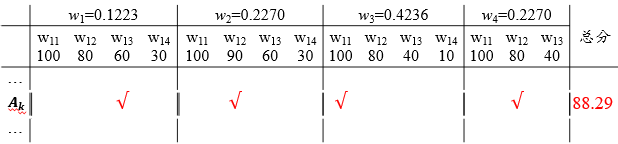
每个申报者根据在准则中所处等级的位置对号入座.
工作4年、能力优秀、品质良好的本科毕业生Ak总分:
60×0.1223+90×0.2270+100×0.4236+80×0.2270=88.29
评定前确定标准分(如80),标准分以上才可以晋升.
层次分析法应用的步骤
建立由目标层、准则层、方案层等构成的层次结构.
构造下层各元素对上层每一元素的成对比较阵.
计算各个成对比较阵的特征根和特征向量,作一致性检验,通过后将特征向量取作权向量.
对各层权向量进行综合,用分层加权和法计算最下层各元素对最上层元素的权重.
层次分析法的广泛应用
应用领域:经济计划和管理,能源政策和分配,人才选拔和评价,生产决策,交通运输,科研选题,产业结构,教育,医疗,环境,军事等.
处理问题类型:决策、评价、分析、预测等.
建立层次结构模型是关键的一步,要有主要决策层参与.
构造成对比较阵是整个工作的数量依据,应由经验丰富、判断力强的专家给出.
广泛应用:
例1.国家实力分析
例2.工作选择
例3.横渡江河、海峡方案的抉择
例4.科技成果的综合评价
正互反阵最大特征根和特征向量的简化计算
精确计算复杂且不必要.
简化计算的思路——一致阵的任一列向量都是特征向量,一致性尚好的正互反阵的列向量都应近似特征向量,可取其某种意义下的平均.
和法——取列向量的算术平均
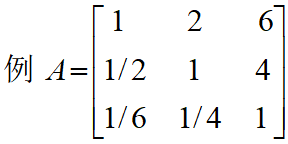

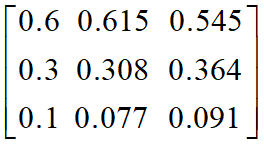

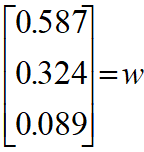
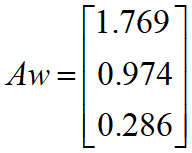
![]()
![]()
精确结果: w=(0.588,0.322,0.090)T, λ=3.010
根法——取列向量的几何平均
幂法——迭代算法
层次分析法的优点
系统性——将对象视作系统,按照分解、比较、判断、综合的思维方式进行决策——系统分析(与机理分析、测试分析并列);
实用性——定性与定量相结合,能处理传统的优化方法不能解决的问题;
简洁性——计算简便,结果明确,便于决策者直接了解和掌握.
层次分析法的局限
囿旧——只能从原方案中选优,不能产生新方案;
粗略——定性化为定量,结果粗糙;
主观——主观因素作用大,结果可能难以服人.


