7.3   循环比赛的名次

问题的提出：

• n支球队单循环赛，每场比赛只计胜负，没有平局.

• 根据比赛结果排出各队名次.

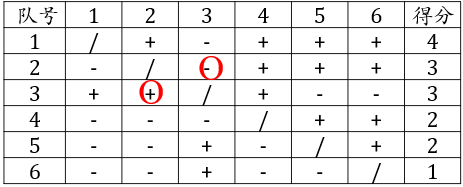
• 6支球队比赛结果(+ ~ 行队胜列队)

• 常用方法：按得分排序1,(2,3),(4,5),6

   2, 3队并列, 4, 5队并列，无法排名!

  又已知3队胜2队，4队胜5队 排名132456 合理吗?

竞赛图（Tournament）

• 竞赛图——每对顶点有且仅有一条有向边相连

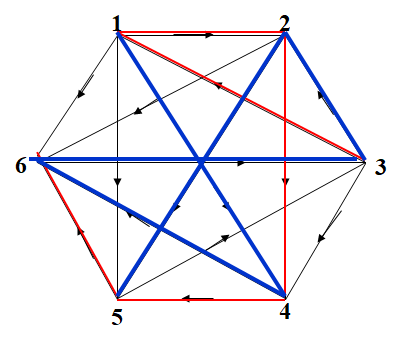
• 竞赛图的性质

  必存在完全路径（按箭头方向通过全部顶点的路径）

• 若存在唯一的完全路径，则由它确定的顶点顺序与按得分排列的顺序一致
  

  如；312456，146325，…… 无法排名

• 不具有唯一的完全路径时：

  双向连通图——从任一顶点出发，至少存在一条有向路径到达另外任一顶点

  其他：不易给出所有队的排名

• 以下只考虑双向连通图

• 双向连通竞赛图的排名

  邻接矩阵

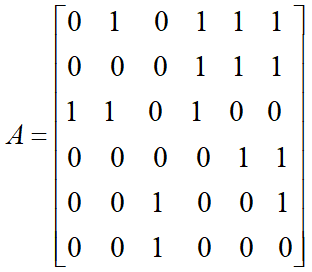
  得分向量，

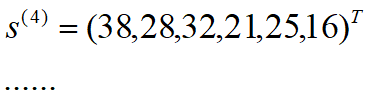
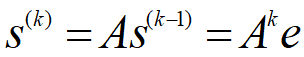• ——k级得分向量，显然更能反映球队的实力

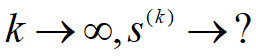• ——极限得分向量（归一化），可以用作排名的依据

• 对于n (>3)个顶点的双向连通竞赛图，存在正整数r，使邻接矩阵A满足Ar>0，A称素阵.

• 素阵A的最大特征根为正单根l，对应正特征向量s*，且

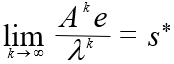
           用s*排名

• 上例中6支球队比赛，已算出2-4级得分向量......

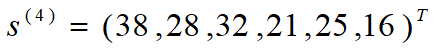• 利用MATLAB的eig命令算出邻接矩阵A的最大特征值l，及其对应的归一化特征向量s*作为排名的依据

• 

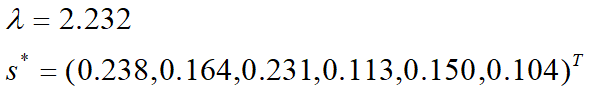
• 排名次序为{1，3， 2，5，4，6}