函数的极限

函数：limit

功能：求取函数的极限

语法：

     limit(f)

     limit(f,x,a)

     limit(f,x,a,'right')

     limit(f,x,a,'left')

说明：第一个指表达式f中自变量趋于0时的极限；第二个指表达式f中自变量x趋于a时的极限；第三个指表达式f中自变量x趋于a时的右极限；表达式f中自变量x趋于a时的左极限。‍

例子1:求                           

syms n;    %syms申明后面的变量为符号变量

y=(1+1/n)^n;

limit(y,n,inf)

ans =

exp(1) 

        例子2:求  

        syms x;

        y=sin(x)/x;

        limit(y,x,0)

        可得结果为：

        limit(y,x,0)

        ans =

        1

例子2:求

syms x;

y=1/(x*(log(x))^2)-1/(x-1)^2;  %log即ln

limit(y,x,1,'right')

可得结果为：

ans =1/12

例 4 研究函数 当 倾于0时的变化规律.

事实上,函数在点附近具有剧烈的震荡性,下面我们在点附近初步来看函数的图像.

x=-1:0.0001:1;

y=sin(1./x);

plot(x,y)

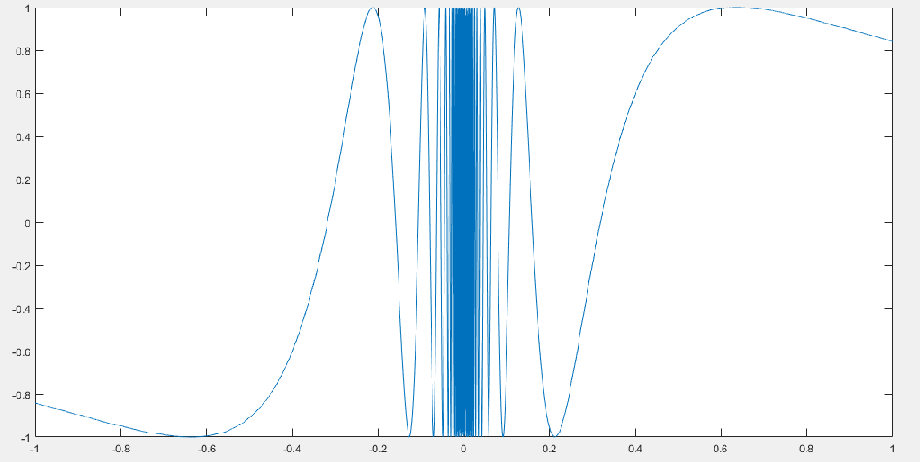
下面我们来计算函数 在 倾于0时的极限.

syms x;

y=sin(1/x);

limit(y,x,0)

ans =

NaN

可以看,这个极限是不存在的.