随机模拟的MATLAB实例

蒙特卡罗(Monte Carlo)方法，也称为计算机随机模拟方法，是一种基于"随机数"的计算方法。假设我们有个y=x^2的表达式，如何用MC方法求得函数在[0,1]区间的定积分呢？定积分可以用面积来求解，也就是通过求箭头下的面积为了衔接方便，照顾新手，给出作图程序吧

x=0:0.01:1;y=x.^2;plot(x,y);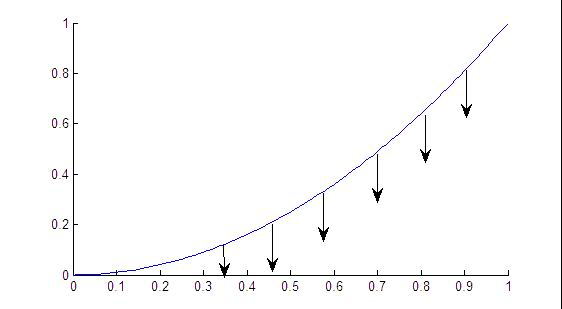
 
MC方法实现非常简单，通过下面的代码就可以

staus=10;

for i=1:4  %4次模拟

point=staus.^i; %模拟的随机点数

RandData=rand(2,point); %根据随机点数，产生随机的(x,y)散点,不明白可以试试   %scatter(RandData(1,:),RandData(2,:))

Below=find(RandData(1,:).^2>RandData(2,:));%寻找位于曲线下的散点

Outcome(i)=length(Below)/length(RandData);%最终结果的表示

end

Outcome =0.3000    0.3600    0.3180    0.3311

从Outcome看，通过不断增加随即点数，结果越与真实值相符
当散点数为10^4时，所得图见下
BelowData=RandData(:,Below);
hold on
scatter(BelowData(1,:),BelowData(2,:))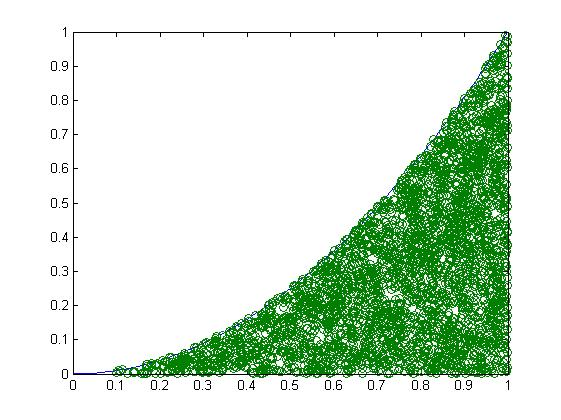


如果我们选取的散点数为10^5，则定积分值为0.3335，所得图形见下（代码略，同上）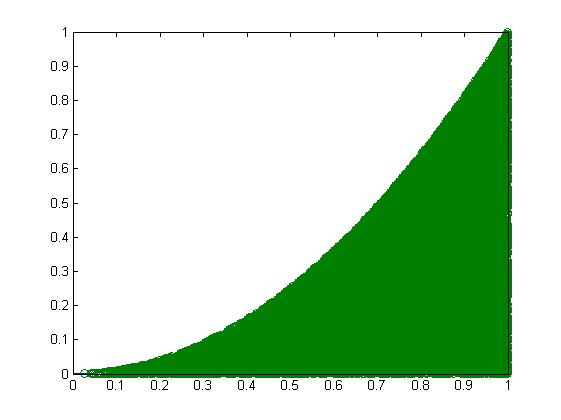


以上是对MC方法最简单的理解，不过思想上是融会贯通的，适合新手学习。所以很明确，MC是基于概率的随机模拟方法。