二分法求根函数

二分法的基本思想

对于区间上连续函数且满足的函数 ，通过不断地把函数的零点所在的区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫二分法

算法设计

给定精确度 $\varepsilon$, 用二分法求函数 $f$ 零点近似值的步骤如下:

1 确定区间$[a,b]$,验证$f(a)·f(b)<0$,给定精确度ξ.

2 求区间$(a,b)$的中点$c$.

3 计算$f(c)$.

(1) 若$f(c)=0$,则$c$就是函数的零点;

(2) 若$f(a)·f(c)<0$,则令$b=c$;

(3) 若$f(c)·f(b)<0$,则令$a=c$.

(4) 判断是否达到精确度 $\varepsilon$ :即若 $|a-b|< \varepsilon$ $,则得到零点近似值$$a$$或者b$,否则重复2-4.

例子

例 : 用二分法求函数 $f(x)=x^3 +1.1x^2 +0.9x-1.4$在区间(0,1)内的实根的近似解(误差不超过$10^{-3}$);

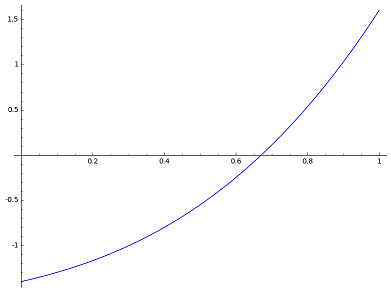
解 注意到 $ f(0)f(1) <0 $ 故函数 $f(x)=x^3 +1.1x^2 +0.9x-1.4$在[0,1]中有根;又因为$f^{'}(x)=3x^2+2.2x+0.9 > 0 $,因此函数 $f$ 在[0,1]中仅有一个零点(也可用fplot 命令显示f(x)的图形得此结论),适合用二分法求根.

MATLAB程序

f = input('f =');

a = input('a = ');

b = input('b = ');

e = input('e = ');

c = (a + b)/2;k=1;

while abs((c))>e

  if f(c)>0

  b = c;

  else 

  a = c;

  end

  c = (a + b)/2;k = k + 1;

end 

[c,k]