学会利用MATLAB中的集合交、并、补运算查找特定元素,编写程序.
1 数独游戏简
数独(sudoku)来自日文,但概念源自“拉丁方块”,据说是18世纪瑞士数学家欧拉发明的.数独游戏在日本和欧美很流行,人们把它作为锻炼脑筋的好方法.游戏规则很简单:一个9×9的大棋盘按九宫格的方式划分成9个3×3小棋盘(9个宫).棋盘上已经填写了1到9若干数字,每行、每列以及每宫中填的数字没有重复.我们不妨把这样一个棋盘称为一个“准数独”,如图23.1(a)就是一个准数独,其中“0”表示空格.游戏的玩法是在准数独的所有空格中填进数字1,2,3…,9,要求每行、每列以及每宫中填的数字没有重复.图(b)是图(a)的一个解答.


(a) (b)
图1 一个简单数独及其解答
2 学习MATLAB命令
集合运算命令
B=unique(A) A为向量,返回的B是与A元素相同但不重复的向量,且向量元素按顺序排列.
C=union(A,B) A ,B为向量时返回A,B作为集合的并C=A∪B.
C=intersect(A,B) A ,B为向量时返回A , B作为集合的交C=A ∩ B.
C=setdiff(A,B) A ,B为向量时返回A , B作为集合的差C=A\B.
3 实验内容
【例1】 编写一个数独游戏程序,并用此程序求解图23.1和图23.2给出的数独.

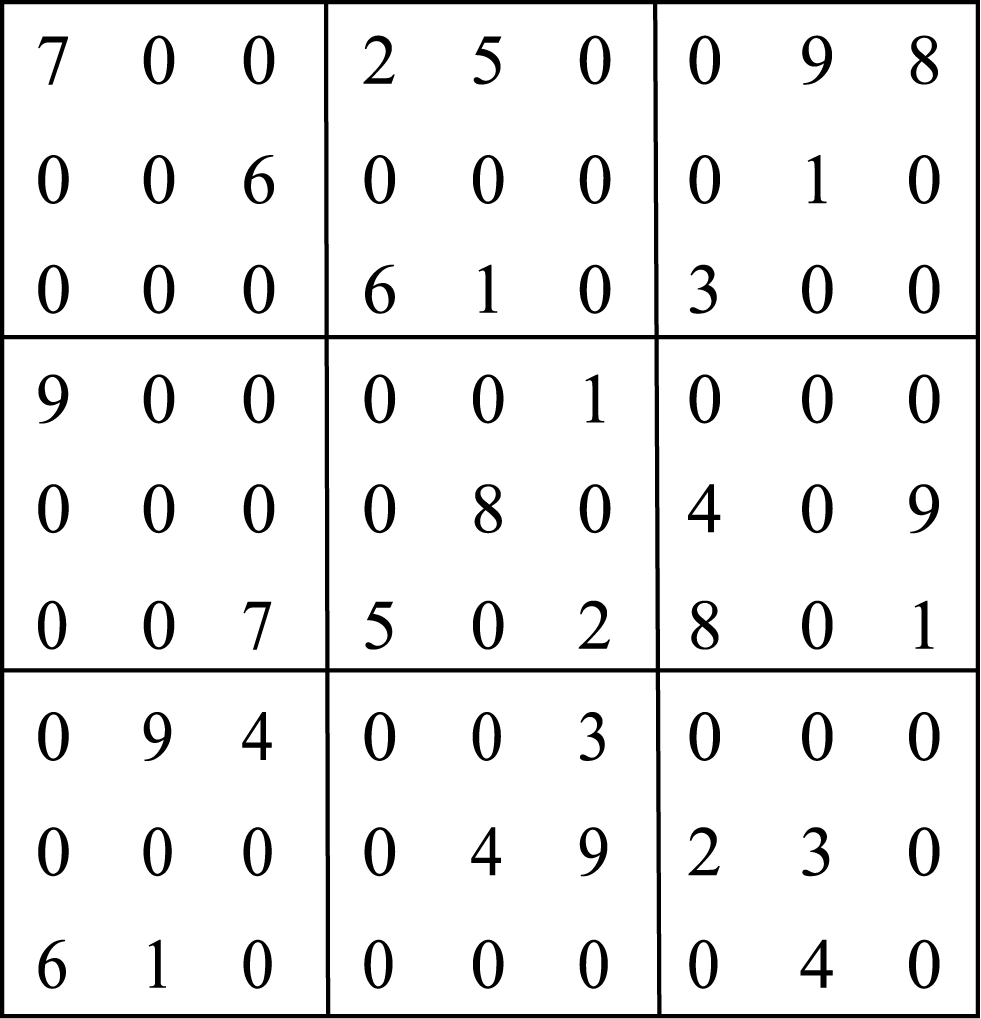
图23.2 一个较为复杂的数独
解 对于空格(i,j),我们只能填那些第i行、第j行以及空格(i,j)所在宫都未出现过的数字.(1)如果发现某一个空格无合适数字可填,则游戏失败;(2)如果某个空格(i,j)只有一个数字可填,则此空格必须填这个数字;(3)如果所有空格都有两个以上的数字可填,则有多种选择,但不是每个选择都保证成功,是否成功要填到最后一个空格才见分晓.
下面是根据上面的想法编写的一段数独游戏程序sudoku.m,简单情况(2)下它可以自动完成.复杂情况(3)下,需要人工介入,程序会给予提示,按提示选择填数,顺利的话一次成功;不然,试几次也能成功(读者也可以尝试编写一个完全自动完成游戏的程序,但程序会长很多).
程序sudoku.m;
function result=sudoku(m)
while 1
m0=ceil(m/9);
1=81-sum(sum(m0));
x=[];flag=1;
for k=1:1
for i=1:9
for j=1:9
if m(i,j)==0
k1=ceil(i/3);k2=ceil(j/3),
m1=m(3k1-2:3k1,3k2-2:3k2);
a=m(i,:);b=m(:,j)';c(1:9)=m1;
d=setdiff(1:9,union(union(a,b),c));
if length(d)==0
flag=0;break
elseif length(d)==1
m(i,j)=d(1);
x=[x;[i,j,d(1)]];
else
r=i;c=j;choise=d;
end
end
end
if flag==0
break
end
end
if flag==0
break
end
end
if flag==0
disp('Impossible to complete!')
break
elseif all(all(m))==0
disp('Choose a number and fill into the blank square,try again!')
m
[r,c]
choise
r=input('r=');
c=input('c=');
m(r,c)=input('m(r,c)=');
else
disp('Success!')
result=m;
break
end
end
对于第一个数独,输入
m=[2 1 0 6 3 0 8 9 0;0 4 0 0 0 7 0 0 5;0 0 0 9 0 0 0 0 7;
0 0 2 0 0 0 0 4 0;4 0 0 1 0 2 0 0 6;0 6 0 0 0 0 1 0 0;
7 0 0 0 0 3 0 0 0;8 0 0 7 0 0 0 6 0;0 3 5 0 9 4 0 2 1]
运行sudoku(m),结果如图23.1(b)所示.
对于第二个数独,输入
m=[7 0 0 2 5 0 0 9 8;0 0 6 0 0 0 0 1 0;0 0 0 6 1 0 3 0 0;
9 0 0 0 0 1 0 0 0;0 0 0 0 8 0 4 0 9;0 0 7 5 0 2 8 0 1;
0 9 4 0 0 3 0 0 0;0 0 0 0 4 9 2 3 0;6 1 0 0 0 0 0 4 0]
运行sudoku(m),在人工选择(9,9)格填7,(8,9)格填6后,程序给出一个答案如图23.3所示,此时答案可能不唯一.
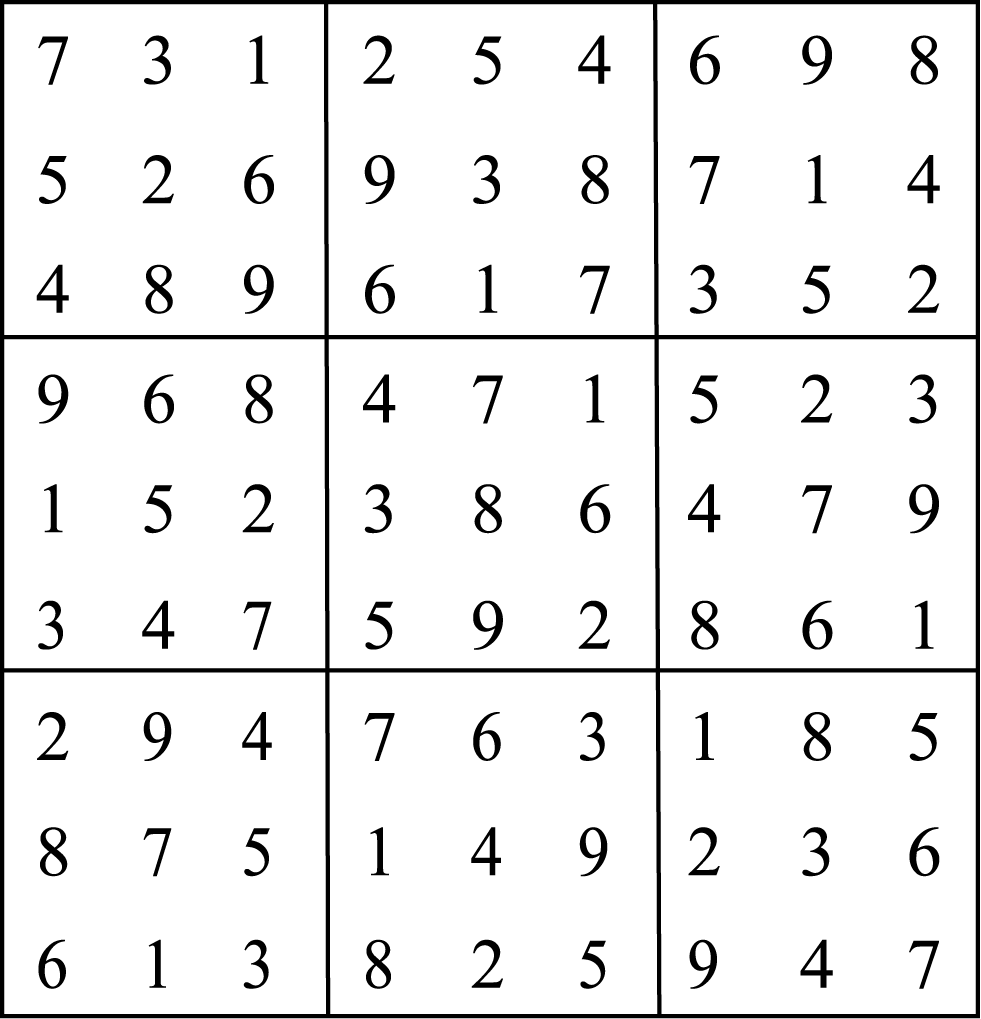
图23.3 对应图23.2的数独的一个解答



