级数

数值级数求和

命令：sum(x)

例1 计算 

x=1:100;y=(1./x).^2;

sum(y)

例2：

x为矩阵：

b=[1 2 3;4 5 6;7 8 9]

b =

  1     2     3
  
  4     5     6
  
  7     8     9

sum(b)

ans =12    15   18

符号级数的计算

例3：计算

syms n k;

symsum(1/n^2,1,inf)

ans =

pi^2/6

例3：计算

syms n k;

symsum(1/n^3,1,inf)

ans =

zeta(3)

例3：计算

for k=1:5syms n;

zeta(2k)=symsum(1/n^(2k),1,inf);end

zeta =

[ 0, pi^2/6, 0, pi^4/90, 0, pi^6/945, 0, pi^8/9450, 0, pi^10/93555]

Taylor展开

taylor(f) %返回函数f 在0处的5阶taylor多项式

taylor(f,x,a) %返回函数f 关于变量x在a处的5阶taylor多项式

taylor(f,x,a,'order',n) %返回函数f 关于变量x在a处的n阶taylor多项式

例 计算 关于0处的10阶的taylor多项式

syms x

taylor(sin(x),x,0,'Order',10)

ans =

x^9/362880 - x^7/5040 + x^5/120 - x^3/6 + x

  x=-5:0.001:5;
  y1=sin(x);
  y2=x.^9/362880-x.^7/5040+x.^5/120-x.^3/6+x;
  plot(x,y1,'b',x,y2,'r')

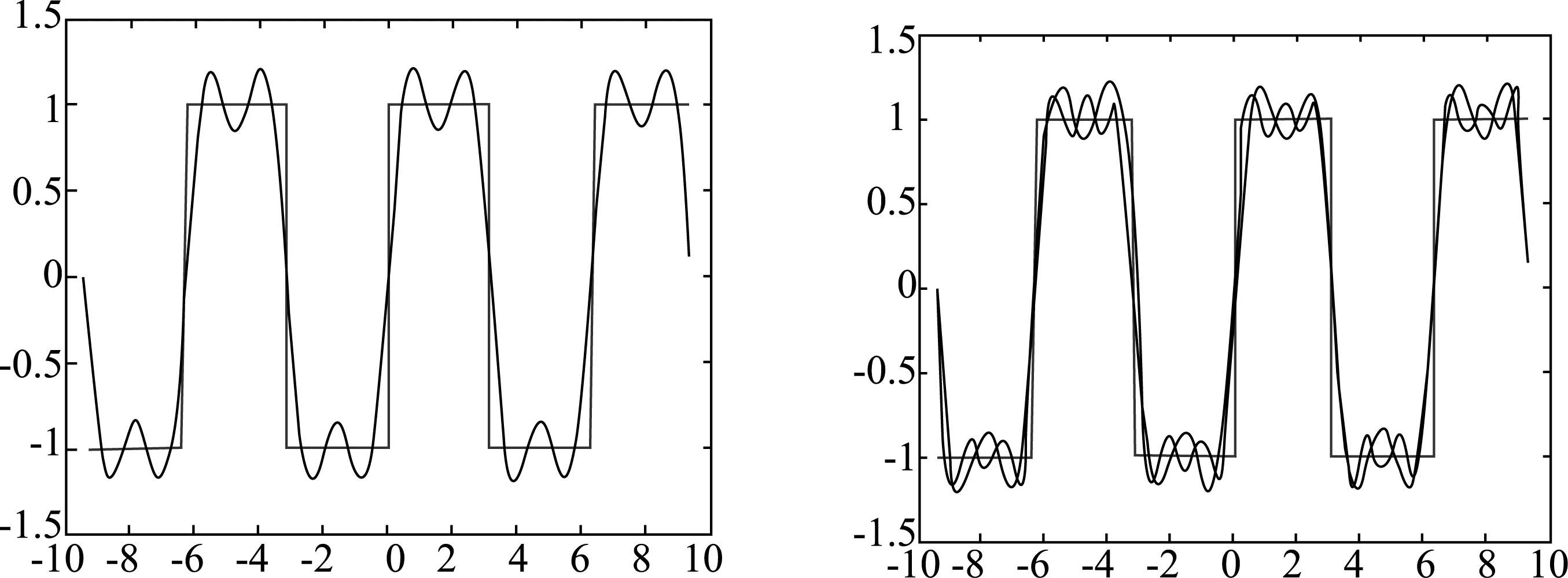
例 设 是以2π为周期的周期函数，它在[－π，π]的表达式是：

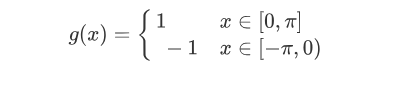
将 展开成傅里叶级数．

因为* 是奇函数，所以它的傅里叶展开式中只含正弦项．输入：

clear；

f＝'sign(sin(x))'；

x＝－3pi：0.1：3pi；

y1＝eval(f)；

plot(x，y1，'r')

pause

hold on

for n＝3：2：9

　　　for k＝1：n

　　　　bk＝－2(((－1)．^k)－1)/(kpi)；

　　　　s(k，：)＝bksin(kx)；

　　　end

　　　s＝sum(s)；

　　　plot(x，s)

　　　pause

　　　hold on

end

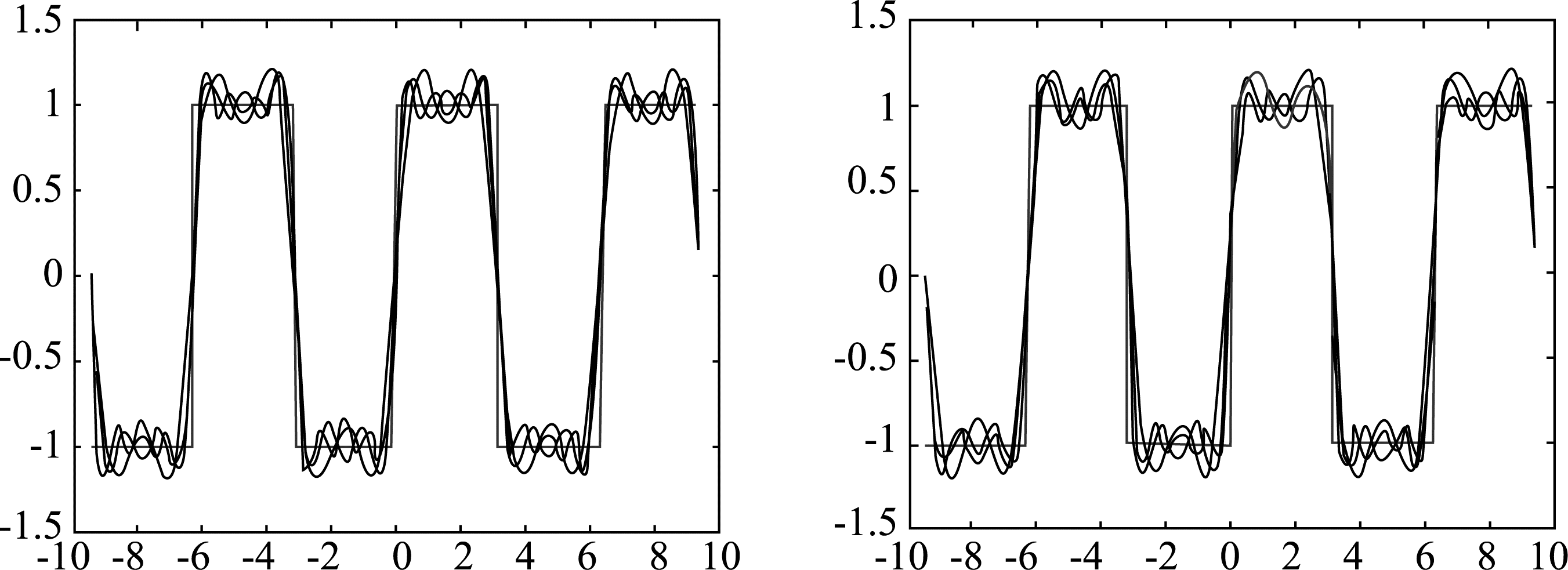
运行结果