观看视频L3.3
一、知识点挖掘：
1、本讲结合 和 的知识，介绍一个能完整求解电路的方法： 法。
2、对于任意含有N个节点，B条支路的电路来说，2B法可诠释如下：
1）第一大部分为B个独立的元件约束：对每条支路可以列出它的元件约束（不仅一个元件的支路等效化处理，即用端口ui关系代替）、共 个。
2）第二大部分为B个拓扑约束：
①对N个节点可以列出它的 方程，共 个；
思考题：为什么是N-1个，扣掉了哪个节点？
②对B-N+1个独立回路可以列出 方程，总共 个方程？
上述方法2B法。
二、归纳总结：总结下2B法的优点和缺点。
三、知识应用：
图6.1所示电路图如下：找出该电路所有节点、网孔，用2B法对该电路列写出电路方程：
图3.1 2B法例图
知识点2：支路电流法
观看视频L3.3
一、知识点挖掘：
1、支路电流法是以 为变量，列写方程进行求解的电路分析方法。
2、对于任意含有N个节点，B条支路的电路来说，可以列出的独立的KCL方程共 个。
3、对于任意含有N个节点，B条支路的电路来说，可以列出的独立的KVL方程共 个。
4、 怎么选取独立节点？
5、怎么选取独立回路？
二、归纳总结：
总结下支路电流法的求解步骤。
对于有n个结点的电路，其独立KCL方程有多少个？以图3.2.1所示电路为例说明：
图3.2.1 KCL的独立方程数 |
图3.2.1有4个结点，6条支路，对结点和支路分别加以编号，支路的（参考）方向如图所示可以任意指定。
对 各结点分别列出KCL方程，有
结 结点1：
结点2：
结点3：
结点4：
由于每条支路都是联接在两个结点之间，每个支路电流必然从其中一个结点流入，而从另一个结点流出，因此，每个支路电流作为一个变量在上述所有KVL方程中均出现两次，一次为正，一次为负。如把上述4个方程中的任意3个方程相加起来，则必将得到另一个方程（相差一个符号）。这表明，有4个结点的电路，只有3个独立KVL方程，这个结论对于具有n个结点电路同样适用，即：
具有n个结点的电路，其独立KVL方程数为（n-1）个。
这样，我们只要对电路中任意（n-1）个结点用KCL列出方程，则这些方程都是独立的，与这些独立方程对应的结点叫做独立结点。
路径：可以用无向图来叙述，从图G的某一结点出发，沿着一些支路连续移动，从而达到另一指定的结点（或原出发点），这样的一系列支路构成了图G的一条路径。一条支路本身也可以称作一条路径。
连通图：当图G的任意两个结点之间至少存在一条路径时，G称为连通图，如图3.2.2就是连通图。
闭合路径：一条路径的起点和终点重合。
回路：一条从起点回到原出发点的路径所经过的结点都不相同时，这条闭合的路径就是图G的一个回路。
图G的两个回路组合起来可以构成另一回路，如图3.2.2所示的图G中，由支路（1、2、6、8）构成的回路可以看作是由支路（1、5、8）和支路（2、5、6）分别构成的两个回路组合起来的，当把两个回路组合起来构成另一回路时，这两个回路的共有支路就相互抵消而不出现在形成的新回路中，同样，把支路（1、5、8）和支路（1、2、6、8）构成的回路组合起来，就可以得到由支路（2、5、6）构成的回路，可见，这三个回路相互是不独立的，因为其中任一回路都可以由其它两个回路导出。
一个具有n个结点和b条支路的的连通图往往具有很多回路。
如图3.2.2所示图G共有13个不同的回路，但它们并不都是独立回路，其中，只有4个独立回路。
图3.2.2 回路 |
平面图：若一个图画在平面上时，除它的各条支路所联接的结点外，其它不再交叉，则这样的图称为平面图。
网孔：平面图中，若一个回路所限定的面积上不包含其它支路，则这样的回路叫做（内）网孔，可以证明，平面图的全部网孔就是一组独立回路，其数目恰好是该图的独立回路数，如图3.2.2中的4个网孔就是该图的一组独立回路，因此，
平面电路中，可取全部网孔作为图的一组独立回路，显然，也可取其余的回路作为一组独立回路。
这时，利用“树”的概念将有助于寻找一个图的独立回路组。
树：连通图G的一个树T是指G的一个连通子图（若G1的每个结点和支路都包含在图G的结点和支路中，则G1为G的一个子图），它包含G的全部结点但不包含回路。
如图3.2.3a，b，c都是图3.2.2所示图G的树，但图d和e则不是G的树，一个连通图有许多不同的树。
图3.2.3 树 |
G的树枝：连通图G中构成树T的支路。
G的连支：连通图G中不属于树T的支路。
例如，图3.2.2所示的连通图G，若选择图3.2.3b 所示的树，则支路1，3，5，6为树支，支路2，4，7，8为连支。
设一个连通图G的结点数为n，支路数为b，可以证明G的任一个树的树支数为（n-1），因为如果把G的支路全部移去，只剩下它的n个结点，为了构成G的一个树，先用一条支路把两个结点联起来，而后，每联接一个新的结点，只需要也只能用一条支路，并保证不形成回路，这样，把n个结点全部联起来所需要的支路树恰好是（n-1）个（第一条支路联接了两个结点），可见:
树支数
连支数
例如图3.2.2所示的图G，树支数为4，连支数也为4（n=5，b=8）。
由于连通图G的一个树不包含回路，且所有结点全部被树支联接。因此，对于任一个树，每加进一连支便形成一个只包含该连支的回路，该回路的其余支路均为树支。
图3.2.4 基本回路 |
例如图3.2.4（a）所示的连通图G，若选择其支路（1，4，5）为树，对这个树分别加入连支2，3，6，便形成了三个回路。
基本回路：只含一个连支的回路称为单连支回路或基本回路。
基本回路组:由全部单连支形成的基本回路构成基本回路组。
基本回路组是独立的，因为它的每一个回路包含了一条为其它回路所没有的支路（连支）。
可以证明，连通图的独立回路数正好等于连支数。所以
对一个结点数为n，支路数为b的连通图，其独立回路数为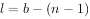
，即连支数。
因此，可以选择基本回路组作为独立回路组，选择不同的树，就可以获得不同的基本回路组。
KVL的独立方程数等于电路的独立回路数。
在图3.2.5所示电路的有向图中，若选择3个独立回路如图所示，则按KVL和图的回路绕行方向有
