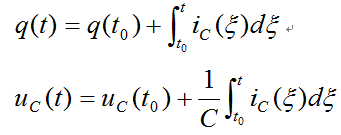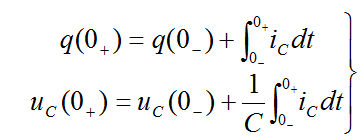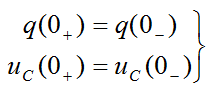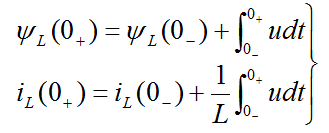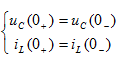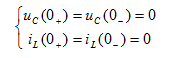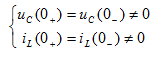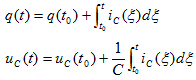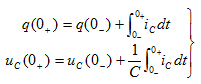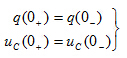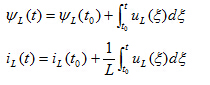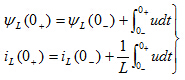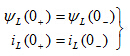当电路中含有储能元件L和C时，由于L、C元件当电路中含有储能元件L和C时，由于L、C元件上电压、电流的约束关系为微分或积分关系：
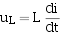
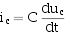（关联参考方向下）
因此，根据KCL、KVL和元件的VCR所建立的电路方程是以电压或电流为变量的微分方程。我们将L元件和C元件又称为动态元件。含有动态元件的电路称为动态电路。
动态电路的一个特征是：当电路的结构和元件的参数发生改变时，可能使电路改变原来的稳定状态而转变到另一种稳定状态。这种转变，一般说来，不能马上完成，而需要经历一个过程。
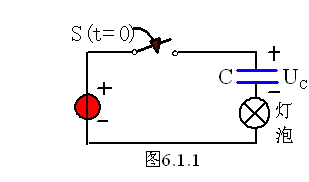
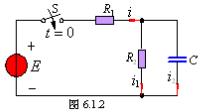
实例：S打开时，灯不亮；S闭合后，为有源电路，C相当于开路，灯应不亮，可为什么S闭合后，灯泡会马上亮起来然后才熄灭？
原因：S闭合改变了电路的工作状态，由稳态1（S打开）转变到稳态2（S闭合后无限长时间），中间经历了被充电的过程。
这种从一种稳态转变到另一咱稳态中间所经历的过程，工程上称为过渡过程。因为过渡过程所经历的时间很短（以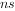
、
、
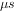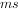计），所以又称为暂态。
8.3换路与换路定理
换路：通常，我们把电路中开关的接通、断开或电路参数的突然变化等统称为“换路”。 并且认为换路是在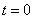
时刻瞬间进行的，并且换路前的瞬间用
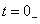表示，换路后的瞬间用
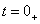表示。本章我们研究的是换路后电路中电压或电流的变化规律，知道了电压、电流的初始值，就能掌握换路后电压、电流是从多大的初始值开始变化的。
如果将换路发生的时刻取为计时起点，即t=0，而以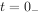
表示换路前的最后一瞬间，它和t=0之间的时间间隔趋近于零；以
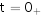表示换路后的最初一瞬间，它t=0之间的间隔也趋近于零，则换路所经历的时间为
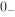到
。
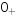对于线性电容来说，在任意时刻t，有
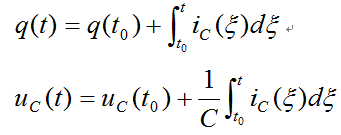
令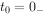
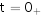，，则得
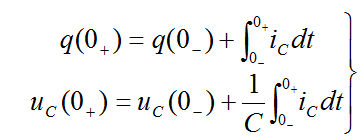（6-1-1）
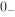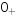如果在换路前后，即到瞬间，电流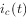
为有限值，则上式中积分项为零。此时，电容上电荷和电压就不发生跃变。有
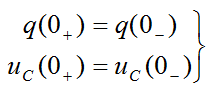（6-1-2）
在线性电感元件上，磁链和电流可写为
令 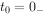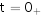，，得
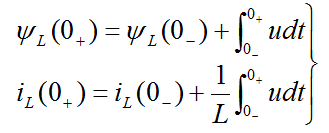（6-1-3）
如果在换路瞬间，即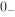到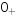瞬间，电感元件的端电压
为有限值，则式（6-3）中积分项为零，电感中磁通链和电流就不发生跃变。即
（6-1-4）
换路定律：
在换路瞬间，电容元件的电流值为有限时，电容电压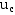
及其电荷量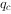
不能跃变；电感元件的电压值为有限时，其电流
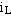及磁通链不能跃变。即
（6-1-5）
除、、、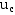
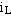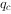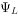四个物理量以外，其余物理量，如
、
、
、
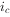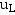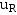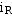以及电压源中的电流、电流源中的电压在换路瞬间都可以跃变。因为它们的跃变不会引起电场各磁场能量的跃变。亦即不会出现无限大的功率。、
必须注意：只有uC 、 iL受换路定律的约束而保持不变，电路中其他电压、电流都可能发生跃
电路响应及其(n-1)阶导数在换路后最初一瞬间的值（即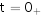时）称为初始值。独立初始值：
、
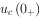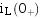
相关初始值：其它可以跃变的物理量的初始值，又称非独立初始值。
独立初始值的求法：
由换路定律确定，即
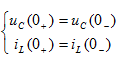
①若换路前电路中的动态元件均未储能，即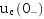
和
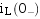均为零，则电路称为零状态电路，具有零初始条件。此时，独立初始值为
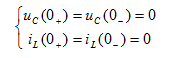
表明，电路在换路后的瞬间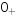（时），C相当于短路，L相当于开路。
②换路前，动态元件均已储能，即
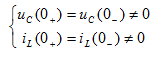
则在换路后的初始瞬间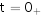（时），C相当于一个电压值为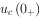的电压源，电压源参考方向与
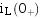相同；L则相当于一个电流值为的电流源，电流源参考方向与
相同。
相关初始值的求解
①先求独立初始值、
②画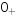等效电路
③得到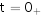等效电路为一个电阻性电路，依KCL、KVL和欧姆定律求相关初始值。上电压、电流的约束关系为微分或积分关系：
（关联参考方向下）
因此，根据KCL、KVL和元件的VCR所建立的电路方程是以电压或电流为变量的微分方程。我们将L元件和C元件又称为动态元件。含有动态元件的电路称为动态电路。
动态电路的一个特征是：当电路的结构和元件的参数发生改变时，可能使电路改变原来的稳定状态而转变到另一种稳定状态。这种转变，一般说来，不能马上完成，而需要经历一个过程。
实例：S打开时，灯不亮；S闭合后，为有源电路，C相当于开路，灯应不亮，可为什么S闭合后，灯泡会马上亮起来然后才熄灭？
原因：S闭合改变了电路的工作状态，由稳态1（S打开）转变到稳态2（S闭合后无限长时间），中间经历了被充电的过程。
这种从一种稳态转变到另一咱稳态中间所经历的过程，工程上称为过渡过程。因为过渡过程所经历的时间很短（以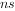、、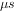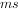计），所以又称为暂态。
如果将换路发生的时刻取为计时起点，即t=0，而以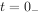表示换路前的最后一瞬间，它和t=0之间的时间间隔趋近于零；以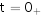表示换路后的最初一瞬间，它t=0之间的间隔也趋近于零，则换路所经历的时间为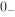到。
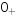对于线性电容来说，在任意时刻t，有
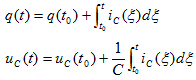
令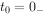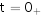，，则得
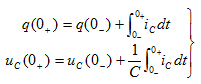（6-1-1）
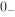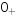如果在换路前后，即到瞬间，电流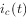为有限值，则上式中积分项为零。此时，电容上电荷和电压就不发生跃变。有
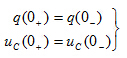（6-1-2）
在线性电感元件上，磁链和电流可写为
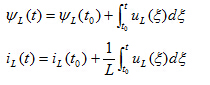
令 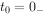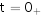，，得
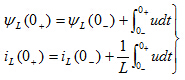（6-1-3）
如果在换路瞬间，即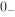到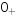瞬间，电感元件的端电压为有限值，则式（6-3）中积分项为零，电感中磁通链和电流就不发生跃变。即
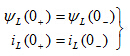（6-1-4）
换路定律：
在换路瞬间，电容元件的电流值为有限时，电容电压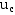及其电荷量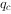不能跃变；电感元件的电压值为有限时，其电流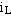及磁通链不能跃变。即
（6-1-5）
除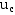、、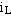、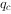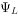四个物理量以外，其余物理量，如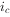、、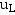、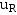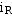以及电压源中的电流、电流源中的电压在换路瞬间都可以跃变。因为它们的跃变不会引起电场各磁场能量的跃变。亦即不会出现无限大的功率。
电路响应及其(n-1)阶导数在换路后最初一瞬间的值（即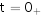时）称为初始值。独立初始值：、
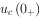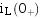
相关初始值：其它可以跃变的物理量的初始值，又称非独立初始值。
独立初始值的求法：
由换路定律确定，即
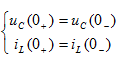
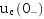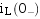①若换路前电路中的动态元件均未储能，即和均为零，则电路称为零状态电路，具有零初始条件。此时，独立初始值为
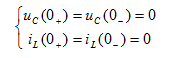
表明，电路在换路后的瞬间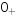（时），C相当于短路，L相当于开路。
②换路前，动态元件均已储能，即
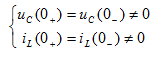
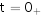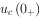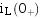则在换路后的初始瞬间（时），C相当于一个电压值为的电压源，电压源参考方向与相同；L则相当于一个电流值为的电流源，电流源参考方向与相同。
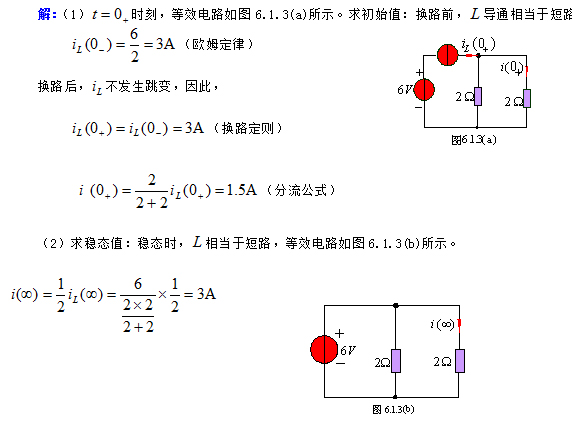
相关初始值的求解
①先求独立初始值、
②画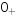等效电路
③得到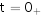等效电路为一个电阻性电路，依KCL、KVL和欧姆定律求相关初始值。
