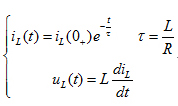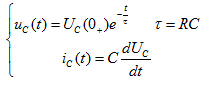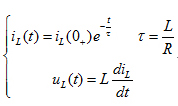零输入响应：零输入是指没有外加电源激励，响应是电路中电压、电流变化规律的统称。零输入响应是指在没有外加电源激励的情况下，仅由储能元件初始储能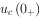
、
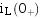引起的响应。
如图6.2.1所示，在换路前，开关S合在1的位置上，电源对电容元件充电，达到稳态时，uC=U。在t=0时，将开关S从位置“1”合到位置“2”，使电路脱离电源，输入信号为零，此时，电容元件上的电压初始值 。在t>0时，电容元件经过电阻R开始放电。 |  |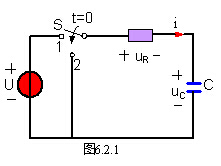
根据KVL，列出t≥0时的电路微分方程
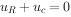
而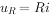
，
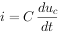代入上式得：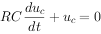
上式为一阶常系数线性齐次微分方程，令它的通解为：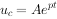
代入方程中，并消去公因子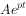
，得出该微分方程的特征方程：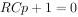
其特征根为 ：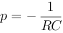
因此，该微分方程的通解为：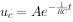
式中A为积分常数，由电路的初始条件确定，即：
，
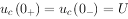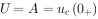
所以 
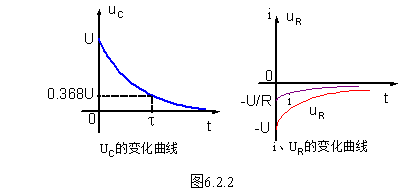
可见，电容在放电时，其电压随时间按指数规律衰减，它的初始值为U，衰减终了为零。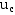
随时间的变化曲线如图6.2.2所示。
RC电路放电过程中电容放电电流和电阻上的电压为
上两式中的负号表示放电电流的实际方向与图中的参考方向相反。画出了
、
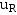随时间变化的曲线。
令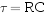 
因为它具有时间的量纲，单位是秒，所以称为RC电路的时间常数。电压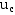衰减的快慢决定于电路的时间常数。
当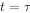
时，电容上电压值为
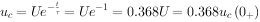
可见时间常数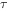
为电容电压衰减到初始值的0.368倍所需要的时间。
1.5 RC零输入响应一般公式：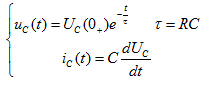
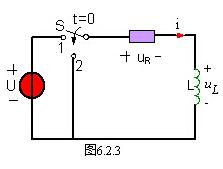
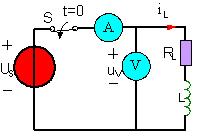
如图 6.2.3 所示，在换路前，开关 S 是合在“1”的位置上，电感元件中通有电流，(
)=
。
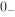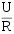在 t=0 时将开关从“1”的位置合到“2”的位置，使电路脱离电源，RL电路被短路。此时，
(
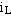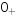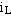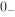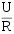)=()=,电感元件已储有能量，逐渐被电阻 R 消耗。
根据KVL得：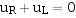
又由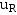 
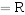. 和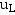 
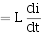代入上式得：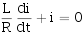
上式为一阶线性常系数齐次微分方程。其特征方程：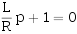
特征根为：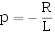
因此，微分方程的通解为：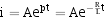
由初始条件可确定：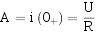
所以，RL电路的零输入响应为：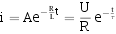
上式中，令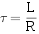 
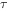； 也具有时间的量纲，称为RL电路的时间常数。
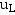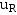、的响应为：
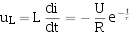
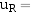R·
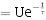
所求 、 、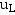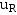随时间而变化的曲线如图所示。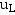为负值表示此时电感元件的实际电压级性与
参考级性相反。
RL零输入响应的一般形式：
