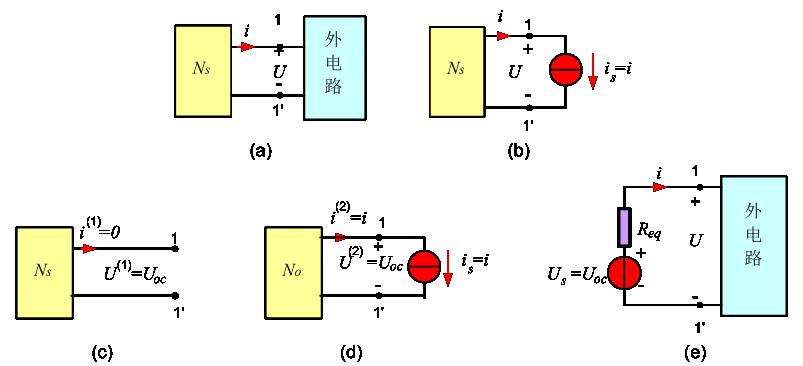
图4.3.2  戴维宁定理的证明过程

设线性有源二端网络与外电路相连，如上图a所示，端口电压为u，电流为i，应用替代定理，将外电路用电流源替代。如图4.3.2（b）所示。

根据叠加定理，令，一端口内所有电源共同作用得图c，则

再令单独作用，一端口内所有电源均不作用，或为无源网络，得图d，此时

   

其中，为无源网络的等效电阻。

依叠加定理，有：

     

得图e。证毕。

可见，戴维南定理确实提供了一种求有源一端口等效电路的普遍适用方法，无论怎样复杂的端口，都可以求出其，，从而代替原网络。

应用戴维南定理的关键，在于求出开路电压和戴维南等效电阻。后者用求输入电阻的方法得到。

1）若除源后的一端口网络只含电阻，不含受控源，用电阻的串、并联以及等效变换求得。

2）分别求出含源一端口网络的开路电压及短路电流，则：

3）若除源后一端口网络含有受控源，则用“外加电源法”求得端口处看入的输入电阻， 

且：

电路含有受控源时，应注意：

1）受控源与其控制量必须同在含源一端口网络内，即受控源与其控制量不能分属于端口内、外，但控制量可以是端口处的电压和电流。

2）含受控源的有源一端口网络，求时要用上述方法2）和3）。在除源时，切不可将受控源像独立电源一样以开路或短路替代，而应将其保留在电路中。

由于戴维南定理将有源一端口简化成了二个电路元件组成的等效电路。因此，它主要应用于： 

1）复杂电路中只需计算电路中某一支路的U、I时；

2）分析某一参数变动的影响(如分析负载如何获得最大功率等)；

3）一些简单的非线性电路(外电路可以是非线性的)。

1）把待求支路以外的部分作为有源二端网络，求出其开路电压作为等效电路中的电压源电压；

2）求等效电阻；

3）用电压源Uoc与等效电阻串联组成戴维南等效电路代替有源二端网络（注意的参考方向），然后计算电路。

把待求支路以外的部分作为有源二端网络，求出其开路电压作为等效电路中的电压源电压；

2）求等效电阻；

3）用电压源Uoc与等效电阻串联组成戴维南等效电路代替有源二端网络（注意的参考方向），然后计算电路。