一、 单位冲激函数
单位冲激函数也是一种奇异函数,通常用符号δ(t)表示,因此单位冲激函数又被称为δ函数。单位冲激函数的定义为
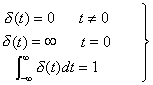
所以单位冲激函数是宽度趋于0、高度趋于∞、面积为1的特殊函数。单位冲激函数可以看作是单位脉冲的一种极限。如图1是一个宽度为Δ、高度为 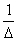 的矩形脉冲,其面积
的矩形脉冲,其面积 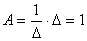 。当宽度Δ不断减小时,矩形脉冲的高度就不断增大,当脉冲宽度Δ趋近于0时,其高度趋近于∞,但其面积不变,仍然为1,该极限情况即为单位冲激函数。由于
。当宽度Δ不断减小时,矩形脉冲的高度就不断增大,当脉冲宽度Δ趋近于0时,其高度趋近于∞,但其面积不变,仍然为1,该极限情况即为单位冲激函数。由于
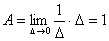 故
故 
单位冲激函数与t轴所包围的面积的大小称为该函数的强度,所以单位冲激函数的强度为1。单位冲激函数的波形如图2所示,用带箭头的线段表示,箭头旁边标注的是它的强度。如果冲激函数为Kd(t),则该冲激函数的强度为K,如图3所示。图4所示波形则是一个延时的单位冲激函数,即


需要说明的是单位冲激函数的积分上、下限也可以不是正、负无穷,只要积分的上、下限包围了函数存在的那一点,积分就等于1,故有下面两式成立
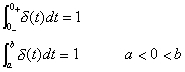
二、 单位冲激函数的主要特性
1、筛选特性或采样特性
当一个连续函数f(t)和单位冲激函数相乘时,由于t≠0时d(t)=0,所以有
f(t) d(t)= f(0) d(t)
故 
由此可推论得

式(1)和式(2)的积分限可缩小,且有


三、单位冲激函数与阶跃函数的关系

四、电路中的冲激函数

图5所示电路,电容上原无储能即uc(0-)=0,当电源电压加到电容元件上后,不难得电容电压为uc(t)=e(t),并且可知uc(0+)=1,即电容电压发生了跳变,此时电容不再遵守uc(0-)= uc(0+)的换路定则。而电容电流

即电容电流为冲激函数。换句话说,电容电压的跳变是冲激电流作用的结果。同理,当冲激电压作用于电感元件时,如图6所示电路,电感电流同样会发生跳变,且

当电感元件的初始储能为零,即iL(0-)=0时, 
因此,单位冲激电压使电感电流从0跳变到了1/L。
