9.8 正弦量的相量表示法

相量法是求解正弦稳态电路的简单方法。由于复数有模和辐角两个要素；而正弦量有幅值、初相和频率三个要素，然而在同一个电路中的所有正弦量均为同频率的正弦量，所以正弦量实际也只有幅值、初相两个要素，所以复数和向量就可以一一对应起来。则为复数的相量表示法提供了可能性。由于向量本身是复数，故对复数作简要回顾。

1．正弦量的相量表示法

将复数乘上因子1∠ωt，其模不变，辐角随时间均匀增加。即在复平面上以角速度ω逆时针旋转，其在虚轴上的投影等于，正好是用正弦函数表示的正弦电流i。可见复数与正弦电流是相互对应的关系，可用复数来表示正弦电流i，记为：

                   ，并称为正弦量的振幅相量。为了与一般复数进行区别，正弦量对应的相量，用大写字母上加一个小圆点。需要注意相量只能表示正弦量，而不是等于正弦量。我们把正弦量的大小和相位画在图上，称为相量图。需要注意：不同频率的正弦量不能画在同一个相量图上，只有同频率的正弦量才能画在同一个相量图上进行相量运算。

正弦量对应的有效值相量为                 ，      振幅（最大值）相量与有效值相量

的关系为          。当正弦量用向量表示之后，正弦量之间的运算就变成了向量之间的运算。如：

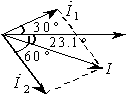
例：求         

解：

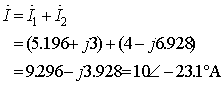
     则对应的向量图为