耦合电感的串联去耦等效
本节主要讲述电感电路的基本分析。含有耦合电感的正弦稳态电路时,仍然采用向量法,KCL的形式不变,但在KVL公式中,应计入由于互感的作用而引起的互感电压,在电路进行等效变换,消去互感,求出它们的去耦等效电路,就可不必计入由于互感的作用而引起的互感电压,最终可达到简化这类电路的分析计算的目的。
含耦合电感的电路有多种形式,下面将对具有不同特点的含有耦合电感的电路进行分析,消去互感,得到消去互感的等效电路。
1. 耦合电感的串联
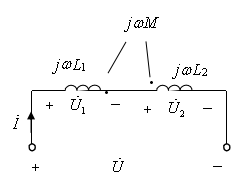
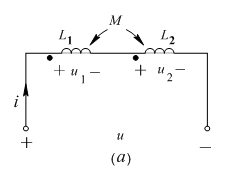
耦合电感的串联方式有两种—顺接串联和反接串 联,电流从两个电感的同名端流进(或流出)称为顺接。如图10.13(a),应用KVL:

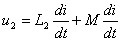
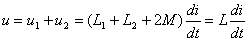 (10.6)
(10.6)
其中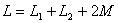 ,由此方程可以得到图10.13(a)的无互感的等效电路如图10.13(c),所以顺接时耦合电感可用一个等效电感
,由此方程可以得到图10.13(a)的无互感的等效电路如图10.13(c),所以顺接时耦合电感可用一个等效电感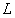 替代。可见顺接时电感增大。
替代。可见顺接时电感增大。
上述对正弦稳态电路,应用相量分析,图10.13(a)的相量模型如图10.14(a).




每一条耦合电感支路阻抗和输入阻抗分别为
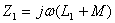


显然顺接时,每一条耦合电感支路阻抗和输入阻抗都比无互感时的阻抗大,这是由于互感的增强作用。
图10.13(b)为串联反接,反接就是同名端相接,应用KVL:



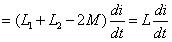 (10.7)
(10.7)
其中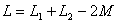 ,由此方程可以得到图10.13 (b)的无互感的等效电路如图10.13(d),反接时耦合电感可用一个等效电感
,由此方程可以得到图10.13 (b)的无互感的等效电路如图10.13(d),反接时耦合电感可用一个等效电感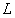 替代,可见反接时电感变小。
替代,可见反接时电感变小。



(c) (d)
图10.13 互感线圈的串联
对正弦稳态电路,应用相量形式分析,图10.13(b)的相量模型如图10.14(b),其相量形式的KVL方程为:



每一条耦合电感支路阻抗和输入阻抗分别为
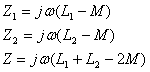
显然反接时,每条耦合电感支路阻抗和输入阻抗都比无互感时的阻抗小,这是由于反接互感相互削弱的作用。