
空心变压器
变压器是利用电磁感应原理传输电能或电信号的器件,它常应用在电工、电子技术中。变压器由两个耦合线圈绕在一个共同的芯子上制成,其中一个线圈与电源相连称为初级线圈,所形成的回路,称为原边回路(或初级回路);另一线圈与负载相连称为次级线圈,所形成的回路称副边回路(或次级回路)。
变压器可以用铁芯也可以不用铁芯。空心变压器(air-core transformer)的芯子是非铁磁材料制成的,其耦合系数较小,属于松耦合。含空芯变压器的电路,一般利用其反映阻抗进行分析计算,下面分析空芯变压器的反映阻抗。
1 反映阻抗
变压器是利用电磁感应原理制成的,可以用耦合电感构成它的模型,其电路模型如图10.21,图中的负载设为电阻和电感串联。变压器通过耦合作用,将原边的输入传递到副边输出。
在正弦稳态下,对图10.21列回路方程有:
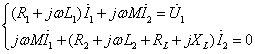 (10.12)
(10.12)
令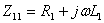 ,
, 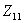 称为原边回路阻抗;
称为原边回路阻抗;
令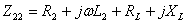 , Z
, Z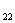 称为副边回路阻抗,
称为副边回路阻抗,
令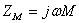 ,
, 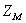 为互阻抗
为互阻抗
则上列方程(10.12)可简写为:
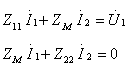 (10.13)
(10.13)
从式(10.13)可求得原边和副边电流:
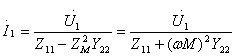 (10.14a)
(10.14a)
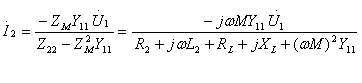 (10.14b)
(10.14b)
显然,如果同名端的位置不同,对初级电流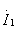 ,由于式(10.14a)中的
,由于式(10.14a)中的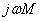 以平方形式出现,不管
以平方形式出现,不管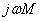 的符号为正还是为负,算得的
的符号为正还是为负,算得的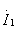 都是一样的。但对于次级电流
都是一样的。但对于次级电流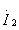 却不同,当同名端位置变化时,
却不同,当同名端位置变化时,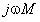 前的符号也变化,
前的符号也变化,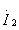 的符号也随着变化。也就是说,如果把变压器次级线圈接负载的两个端钮对调一下,或是改变两线圈的相对绕向,流过负载的电流将反相1800度。在电子电路中,如对变压器耦合电路的输出电流相位有要求,应注意线圈的相对绕向和负载的接法。
的符号也随着变化。也就是说,如果把变压器次级线圈接负载的两个端钮对调一下,或是改变两线圈的相对绕向,流过负载的电流将反相1800度。在电子电路中,如对变压器耦合电路的输出电流相位有要求,应注意线圈的相对绕向和负载的接法。
式(10.14)中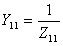 ,
,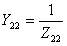 。式(10.14a)中的分母
。式(10.14a)中的分母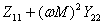 是原边的输入阻抗,其中
是原边的输入阻抗,其中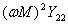 称为反映阻抗(reflected impedance),或引入阻抗,它是副边的回路阻抗通过互感反映到原边的等效阻抗。这就是说次级回路对初级回路的影响可以用反映阻抗来计及。引入阻抗
称为反映阻抗(reflected impedance),或引入阻抗,它是副边的回路阻抗通过互感反映到原边的等效阻抗。这就是说次级回路对初级回路的影响可以用反映阻抗来计及。引入阻抗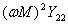 的性质与
的性质与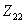 相反,即感性(容性)变为容性(感性)。
相反,即感性(容性)变为容性(感性)。
式(10.14a)可以用图10.22(a)所示的等效电路表示,它是从电源端看进去的等效电路,称为原边等效电路。
应用同样的分析方法分析式(10.14b),可以得出图10.22(b)所示等效电路;它是从副边看进去的含源一端口的一种等效电路,称为副边等效电路。其中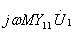 是当
是当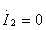 时,2和2
时,2和2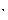 端的开路电压
端的开路电压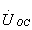 ,称为等效电源电压,它是初级电流
,称为等效电源电压,它是初级电流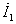 通过互感而在次级线圈中产生的感应电压:
通过互感而在次级线圈中产生的感应电压:

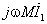 是初级电流
是初级电流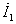 通过互感在次级线圈中产生的感应电压,次级电流就是
通过互感在次级线圈中产生的感应电压,次级电流就是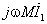 作用的结果.
作用的结果.
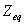 是从2和
是从2和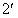 端看进去的等效阻抗,令
端看进去的等效阻抗,令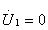 得到:
得到:
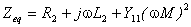
变压器还有其它形式的等效电路,这里不再介绍。

图10.21空芯变压器的电路模型

(a)原边等效电路 (b) 副边等效电路
图10.22 空芯变压器的等效电路

1. 直接列方程法
[例10.7] 电路如图10.23所示,已知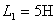 ,
,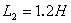 ,
,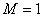 H,
H, 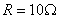 ,
,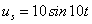 V,求稳态电流
V,求稳态电流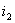 。
。
[解]:考虑互感电压,对电路列回路方程:

解方程,得:


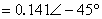 A
A
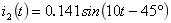 A
A
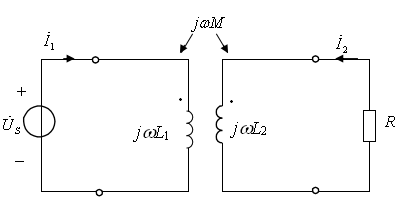
图10.23 例题10.7电路图
必须注意的是,按KVL列回路方程时,应计入由于互感作用而存在的互感电压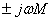 ,应正确选定互感电压的正负号。
,应正确选定互感电压的正负号。
[例10.8] 电路如图10.24(a)所示,图(a)为含有耦合电感的电路,试列写电路的回路电流方程。
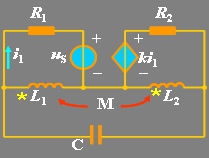
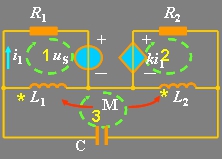
(a) (b)
图10.24 例题10.8电路图
[解]:设网孔电流如图10.24(b)所示,为顺时针方向,则回路方程为:

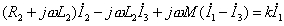

注意: 列写有互感电路的回路电流方程时,注意不要遗漏互感电压。
2. 等效电路分析法
这种分析方法就是采用10.3.1中的反映阻抗的方法,将含有空芯变压器的电路变换成原边等效电路或副边等效电路,在等效电路中列电路方程,再进一步求解。
[例10.9] 电路如图10.25(a),已知 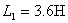 ,
, 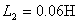 ,
,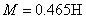 ,
, 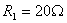 ,
, 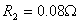 ,
,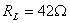 ,
,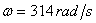 ,
, 
求: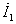 、
、
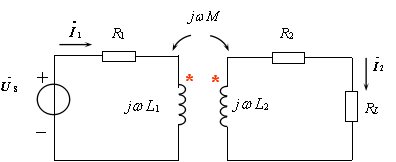
[解]:图10.25(a)的空心变压器原边等效电路如图10.25(b)。
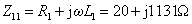


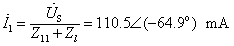
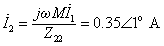

(a)
 (b)
(b)
图10.25 例题10.9电路图
[例10.10] 已知图10.26(a)所示电路中,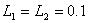 mH,
mH,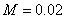 mH,
mH,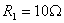 ,
, 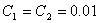 mF ,
mF , 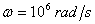 ,
,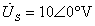 , 问:
, 问: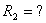 时能吸收最大功率,并求最大功率。
时能吸收最大功率,并求最大功率。
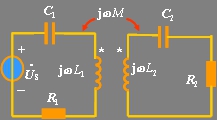

(a) (b) (c)
图10.26 例题10.10电路图
[解]:
解法 1:因为
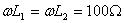
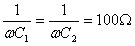
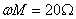
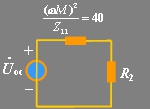
所以原边自阻抗为: 
副边自阻抗为: 
原边等效电路如图(b)所示,引入阻抗为:

因此当 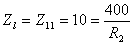 即
即 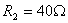 时吸收最大功率,最大功率为:
时吸收最大功率,最大功率为:

解法2:
应用图(c)所示的副边等效电路,得


因此当 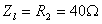 时吸收最大功率,最大功率为:
时吸收最大功率,最大功率为:

