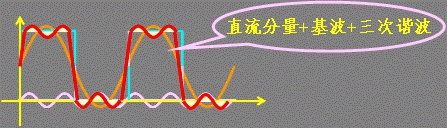
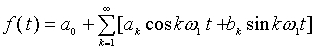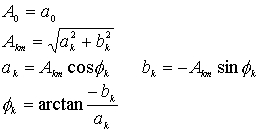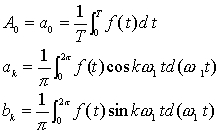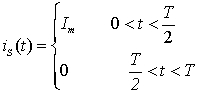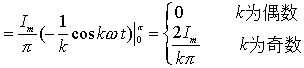非正弦周期函数分解为傅里叶级数
-
1 课前导学
-
2 课程视频
-
3 课程内容
-
4 典型例题
上一节
下一节
知识点2: 非正弦周期信号的傅里叶级数分解
导学关键:通过知识点挖掘了解谐波分析法的思想;了解非正弦周期信号可以通过傅里叶级数分解为直流信号和正弦交流信号;了解傅里叶级数展开式的两种具体形式中各系数的计算,以及两种傅里叶级数展开式之间的关系。通过归纳总结引导学生对傅里叶级数展开进行深度理解,了解不同特点的信号傅里叶级数展开式中哪些系数为零,逐步培养学生观察能力、分析能力。
观看学习通视频14.2
一、知识点挖掘:(课前学习)
1、本视频介绍了非正弦周期信号满足 条件时可以展开为傅里叶级数 的形式。
2、在傅里叶级数展开式 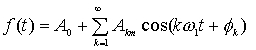 中,常数项称为 、其余各项称为 、并把频率与原周期函数相同的谐波分量称为 、其余谐波分量称为 。
中,常数项称为 、其余各项称为 、并把频率与原周期函数相同的谐波分量称为 、其余谐波分量称为 。
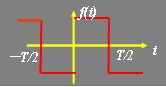
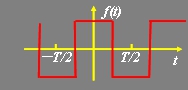
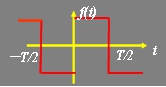
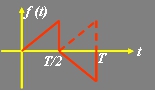
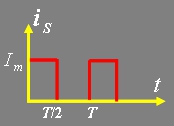
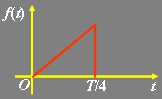
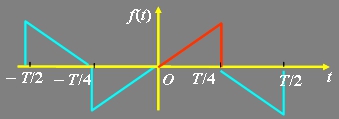
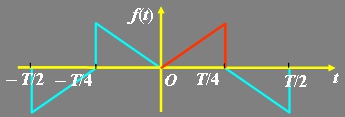
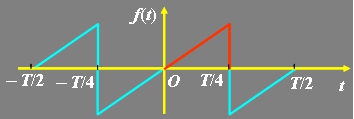
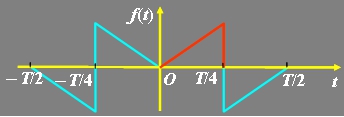
3、图示函数具有 对称性,其傅里叶级数展开式中,系数 为零,因此 傅里叶级数展开式中不含 项。
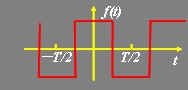
二、归纳总结:(课中总结)
根据图示函数的波形,判断函数具有哪种对称性?判断出其傅里叶级数的系数中哪个系数为零,展开式中含有哪些项?最后计算出不为零的系数,并对信号的傅里叶级数展开过程做总结。