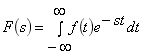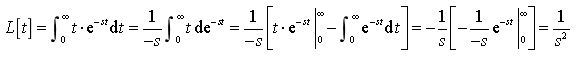知识点1:拉普拉斯变换
导学关键:本节重点讲解拉普拉斯变换的定义。首先引出积分变换的思想,帮助同学们建立积分变换与工程问题解决方法之间的关系。提出经典法和运算法两种求解动态电路的思路,同学们在后面的小节中会重点学习。引出拉普拉斯正反变换的定义及象函数存在的条件,请对比傅里叶变换的条件体会两者的区别于联系。最终用三个最典型的拉氏变换对的例题巩固正反变换公式计算。
观看视频14.1
一、知识点挖掘:
1、动态电路的时域分析法所建立的电路方程是 ,因此适合于一阶电路和简单的二阶电路,对于高阶电路用时域经典法分析时,确定 和 很麻烦,因此引入拉普拉斯变换的复频域分析法,可以简化分析的计算。
2、拉普拉斯变换是一种 ,它可以将时域描述动态过程的常系数线形微分方程变换为复频域的 ,使分析计算易于进行
3、 时域函数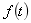 的拉氏变换为
的拉氏变换为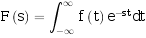 : 其中
: 其中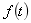 称为
称为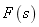 的 ,
的 , 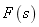 称为
称为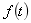 的 ,由原函数变换为象函数的过程,称为 。
的 ,由原函数变换为象函数的过程,称为 。
4、拉普拉斯正变换中,为了使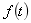 的拉氏变换存在,变量s的实部
的拉氏变换存在,变量s的实部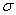 应该为 。
应该为 。
5、 单位阶跃函数f(t)=e(t)的像函数为 ,单位冲激函数f(t)=d(t)的像函数为 。
二、归纳总结:
求出单位阶跃函数f(t)=e(t)、单位冲激函数f(t)=d(t)的像函数,并从求出的像函数分析和归纳一下时间域的微积分对应于复频域的什么运算?

动态电路复频域分析
一、基本要求
1.了解拉普拉斯变换的定义,明确其基本性质和应用拉普拉斯变换分析电路的概念。
2.会查表得出电路中常用函数的拉氏变换;掌握运用部分分式展开和查表方法进行拉普拉斯反变换。
3.掌握基尔霍夫定律和元件伏安关系的复频域形式,复频域阻抗与导钠,会建立动态电路的复频域模型。
4.熟练掌握应用复频域方法分析电路中过度过程的方法和步骤。
(一)关于变换域分析法的概念
动态电路的分析,除有时域分析法外,也还有变换域分析法,应用拉普拉斯变换的复频域分析法,是一种主要的变换域分析法。时域分析法易于一阶电路和简单二阶电路的分析,但对于高阶电路采用时域经典法分析计算时,确定初始条件和积分常数计算很麻烦,然而,这时应用拉普拉斯变换的复频域分析法,可以简化分析的计算。
拉普拉斯变换是一种积分变化,它可以将时域描述动态过程的常系数线形微分方程变换为复频域的代数方程,在复频域求解代数方程,得出待求响应量的复频域函数,最后经拉氏反变换为所求解的时域响应。这种变换分析方法,其实质就是时域问题变换为复频域来求解,使分析计算易于进行。
应用拉普拉斯变换分析动态电路,有两种方法,即变换方程和变换电路法。前者是将描述动态电路的微分方程,经拉氏变换为复频域代数方程,在复频域求解后,反变换为时域响应;后者是将时域电路直接变换为复频域电路,即S域模型。根据S域模型进行分析计算,得出响应量的S域形式,最后反变换为时域响应。本课程主要讨论后一种方法。
1.拉普拉斯变换及其基本性质
1. 拉普拉斯正变换
时域函数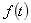 的拉氏变换为:
的拉氏变换为: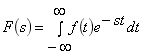 其中
其中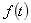 称为
称为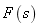 的原函数,
的原函数,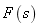 称为
称为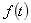 的像函数。
的像函数。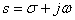 是复数,即复频率,故象函数
是复数,即复频率,故象函数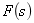 是复频域函数或S域函数,其变量是复数S,而不是时间t。由原函数变换为象函数,称为拉氏正变换。拉氏正变换的符号为
是复频域函数或S域函数,其变量是复数S,而不是时间t。由原函数变换为象函数,称为拉氏正变换。拉氏正变换的符号为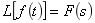
其中s的实部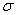 应该为足够大的正数,使函数
应该为足够大的正数,使函数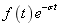 的幅度在t趋向无穷大时能衰减到零,既满足
的幅度在t趋向无穷大时能衰减到零,既满足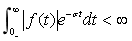 (即绝对可积),
(即绝对可积),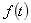 的拉氏变换才存在,
的拉氏变换才存在,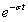 起了收敛作用,称为收敛因子。电工技术中遇到的电量函数,一般都可以进行拉普拉斯积分变换,从而奠定了应用拉氏变换分析电路的基础。
起了收敛作用,称为收敛因子。电工技术中遇到的电量函数,一般都可以进行拉普拉斯积分变换,从而奠定了应用拉氏变换分析电路的基础。
实际中,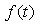 为有始信号(因果信号),
为有始信号(因果信号), 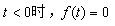 ,所以
,所以
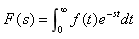 ——单边拉氏变换,此处0意思为0-。
——单边拉氏变换,此处0意思为0-。
例:求以下函数的象函数。
(1) 单位阶跃函数f(t)=e(t) (2) 单位冲激函数f(t)=d(t) (3)指数函数f(t)=e at (4)函数t
解:(1) 单位阶跃函数e (t) 的象函数
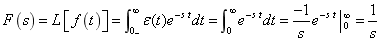
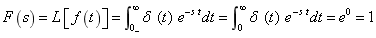 (2) 单位冲击函数d (t) 的象函数
(2) 单位冲击函数d (t) 的象函数
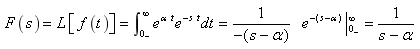 (3) 指数函数eat和
(3) 指数函数eat和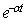 的象函数
的象函数

(4)函数t的象函数
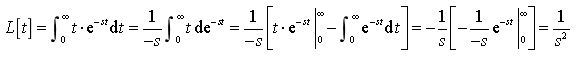
我们知道的东西是有限的,我们不知道的东西则是无穷的。
——拉普拉斯
一、拉普拉斯变换与傅里叶变换的区别
傅里叶变换说的是自然界的很多现象,都可以用三角函数进行分解。
复指数函数eiωt代表一个连续旋转的圆。
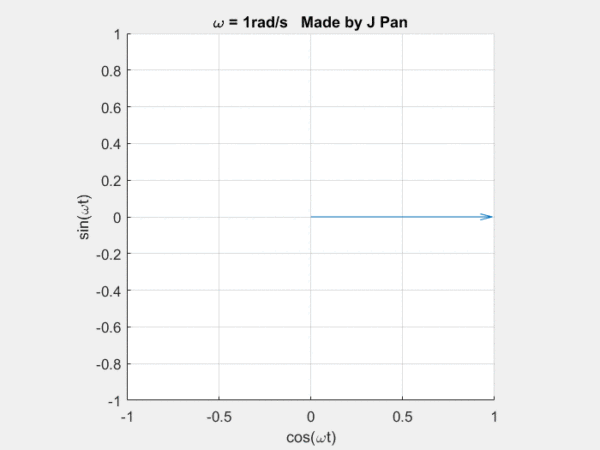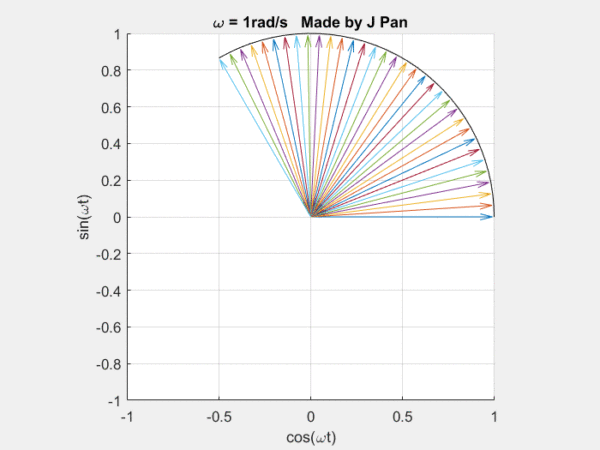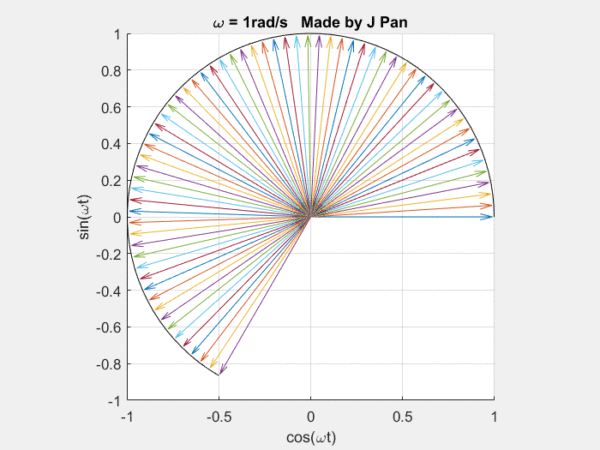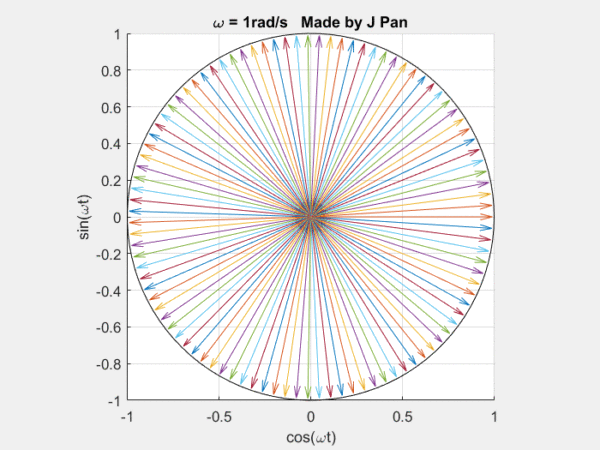
因此,{eiωt} 可以看成是一组连续旋转的曲线,幅值永远为1,频率一直在变。很多曲线,都可以用这些不同频率,连续旋转的圆,通过线性叠加得到。
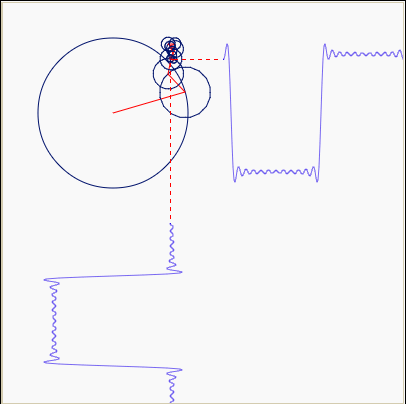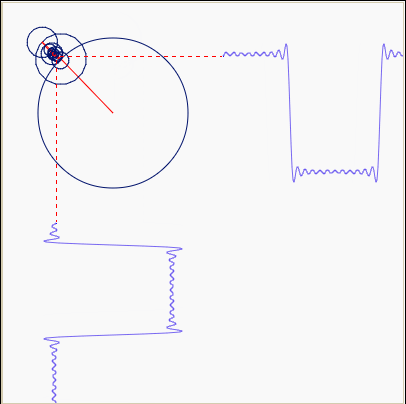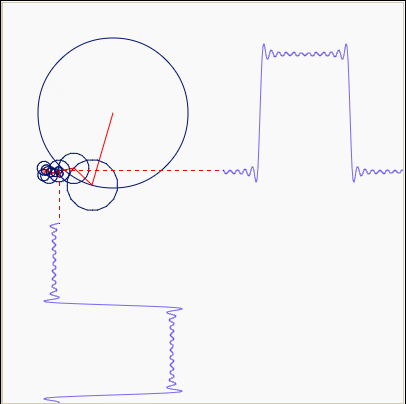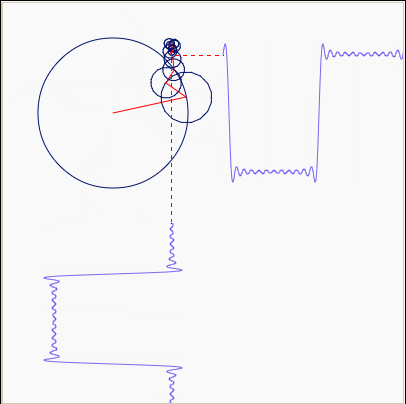
于是就可以很好的解释拉格朗日和傅里叶之间的争论了——拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号,棱角处会有很小高频波动(吉布斯现象)。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅里叶也是对的。一个从数学家的角度,一个从工程师的角度。
傅里叶变换能帮我们解决很多问题,一经问世后便受到广大工程师们的喜爱,因为它给人们提供了一扇不同的窗户来观察世界,从这个窗户来看,很多事情往往变得简单多了。但是,傅里叶变换有一个很大局限性,那就是信号必须满足狄利赫里条件才行,特别是那个绝对可积的条件,一下子就拦截掉了一大批函数。数学家们把不满足绝对的可积的函数乘以一个快速衰减的函数,这样原函数也衰减到零了,从而满足绝对可积,这就是拉普拉斯变换。
![]() 的拉氏变换为
的拉氏变换为 : 其中
![]() 称为
称为![]() 的 ,
的 , ![]() 称为
称为![]() 的 ,由原函数变换为象函数的过程,称为 。
的 ,由原函数变换为象函数的过程,称为 。![]() 的拉氏变换存在,变量s的实部
的拉氏变换存在,变量s的实部![]() 应该为 。
应该为 。