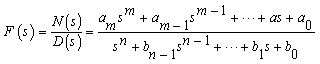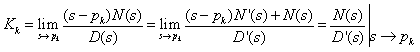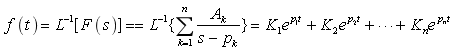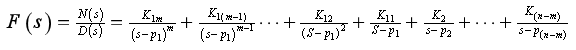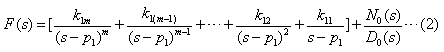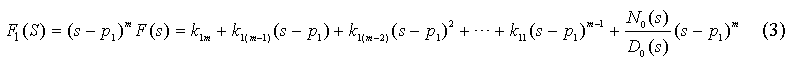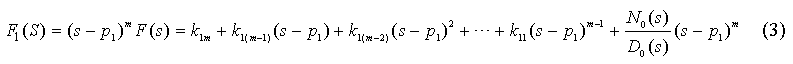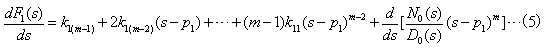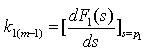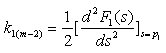知识点3: 拉普拉斯反变换

导学关键：通过知识点挖掘了解拉普拉斯反变换的定义，知道拉普拉斯反变换定义式是一个复变函数的积分变换，因此了解部分分式展开法的重要性；了解拉普拉斯反变换的部分分式展开法的各种情况，学会求简单函数的拉普拉斯反变换；通过归纳总结引导学生对拉普拉斯反变换的部分分式展开法的三种情况进行熟练掌握，逐步培养学生观察能力、总结能力。

观看视频14.3

一：知识点挖掘：

1、拉普拉斯反变换的定义法是直接进行拉氏反变换的积分，是一种        ，运算比较困难。

2、拉普拉斯反变换的部分分式展开法，是将复杂象函数分解为若干        之和，然后分别求取原函数，这种方法适用于象函数是      的情况。

3、像函数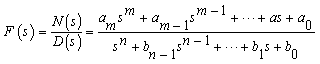其中都是正整数且         ，即是真分式。

4、的根，若为n个不同的单实根则便可展开部分分式为          。待定常数 为          。

5、的分母多项式的根有       个，均为     根，因此可得原函数为           。                  

6、分母多项式，如果含有复数，复数根一般都是以        出现的。如果有一对共扼复极点，，，则待定常数，仍按       情况方法进行计算得出。因 F(s) 是         之比，故 k1,  k2 也应该为        。

7、求 的反变换为           。

二、 知识归纳：

   求以下三个时间函数的像函数  

并对以上三种情况下分母多项式的根的情况与原函数解的形式做归纳，总结两者之间的对应情况。并试着把解的形式与时域函数的波形对应起来。

 拉普拉斯反变换

1. 拉普拉斯反变换定义

复频域函数可经反积分变换为原函数，即

由象函数经过上式积分求出原函数，称为拉氏反变换。拉氏反变换的符号为

应用拉普拉斯变换分析线性动态电路时，要经过拉氏正变换和拉氏反变换两个重要步骤。正变换一般可以根据原函数查表得出它的象函数，比较简捷。但是，经过复频域分析计算得出原函数，往往比较复杂，因为拉斯反变换是一个复变函数的积分，计算起来相当困难。因此，求取较复杂象函数的原函数的拉氏反变换，通常有两种方法，即定义法和部分分式展开法。定义法是直接进行拉氏反变换的积分，这是一种复变函数积分，运算比较困难。部分分式展开法，是将复杂象函数分解为若干简单象函数之和，然后分别查表求取原函数，这种方法适用于象函数是有理函数的情况。在集总线性电路中，常见的响应量电压和电流的象函数往往是S的有理函数。因此，它的拉氏反变换，可以将象函数展开为部分分式后，再逐项反变换为原函数。

2.拉氏反变换的部分分式展开法

如果象函数是S的有理数，它可以表示 两个S的多项式之比，即

若都是正整数，且,即是真分式。这时分母多项式可以用代数分解定律，求出的根，即的极点，有如下三种情况。

1.单根情况

，得出n个不同的单实根  .则便可展开部分分式为

 待定常数 ，可以在上式双边同乘再令式中， 

因为等式左边分母中含这个因子，等式右边为

 可得：

计算时，也可用另一种方法，因为而是分母的根，所以

变为型不定式，由罗比达法则

计算得出待定常数后，根据部分分式，两边取拉普拉斯逆变换并利用线性性质得：     

2.复根情况

分母多项式，得出含有复数根，复数根一般都是以共扼形式出现的。如果有一对共扼复极点，         

   ，，则象函数为

上部分分式中的待定常数，仍按单极点情况方法进行计算得出。因 F(s) 是实系数多项式之比，故 k1,  k2 为共轭复数，设含共轭复根的两项可合为一项          

计算出部分分式各项的待定常数后，便可逐项进行拉氏反变换求出原函数，

 则

3.多重极点情况

若分母，得出含为m个重根时，则的部分分式展开为

计算上部分分式中重积点各项的m个待定常数的一般公式为         

对式（2）乘以得

令得

将（3）式对s再求导一次,并令

得：    将式（5）对s取导一次，再令

   以此类推

其余单极点项的待定常数，仍按单极点情况方法进行计算。

部分分式各项的待定常数确定后，便可逐项进行拉氏反变换得出原函数为

    拉氏反变换是学习中的难点，对以上三种情况确定部分分式各项待定常数的方法，应通过例题和做习题来掌握。

例：求  的原函数

解： 

的根分别为                  

同理

则故

 例：求   的反变换

解：

得  

则

 则

 例：求  的反变换

 解： 有和

 则