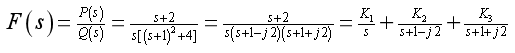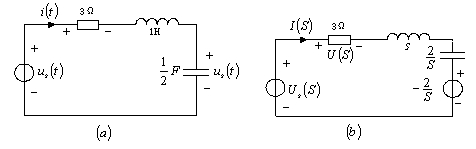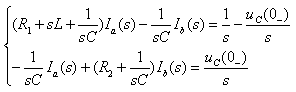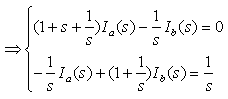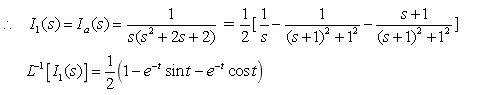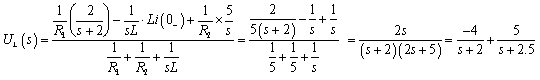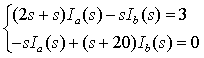知识点2: 应用拉普拉斯变换法分析线性电路
导学关键:通过知识点挖掘了解线性动态电路S域分析法的基本步骤,要格外注意电感和电容元件由于初始状态产生的附加电压源和附加电流源的参数和参考方向;通过归纳总结引导学生对动态电路的S域分析法进行熟练掌握,逐步培养学生动手能力和用理论解决问题的能力。
观看视频14.5
一:知识点挖掘:
1、在作S域模型时,电感和电容元件由于初始状态产生的附加电压源和附加电流源是否存在取决于元件的 是否为零,同时电容电压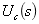 是复频域阻抗
是复频域阻抗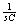 与 串联支路两端的电压,电感电压
与 串联支路两端的电压,电感电压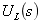 则是 与附加电压源
则是 与附加电压源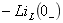 串联支路两端的电压,并要正确标定它们的参考方向。
串联支路两端的电压,并要正确标定它们的参考方向。
2、在根据S域分析法中,以 、 和元件的VAR的S域形式为依据,应用等效化简、节点分析法、网孔分析法、叠加定律和戴维南定律应用等基本分析方法进行分析计算,得出待求电量的象函数。
二、归纳总结:
写出线性动态电路S域分析法的基本步骤,以及整个过程中需要注意的关键点。并通过与时域分析相比归纳总结S域分析法的优点有哪些?
三、知识应用:
1、 应用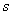 域分析法求一般二阶电路的阶跃响应。如14-2(a)所示电路,求阶跃响应
域分析法求一般二阶电路的阶跃响应。如14-2(a)所示电路,求阶跃响应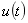 和
和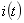
解题关键:本题是一般直流二阶电路求阶跃响应,即零状态响应。作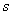 域模型时,初始状态为零,电感元件和电容元件
域模型时,初始状态为零,电感元件和电容元件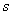 域模型中没有附加电压源。然后根据
域模型中没有附加电压源。然后根据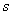 域分析的步骤,首先作出时域电路的
域分析的步骤,首先作出时域电路的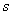 域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。
域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。
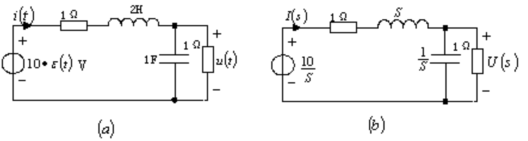
图14-2
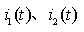 2、求下图所示电路的零状态响应, , 其中,
2、求下图所示电路的零状态响应, , 其中,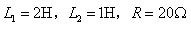
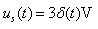 。
。


解题关键: 此题若用时域法求解,不论是求初始值,还是求稳态值都比较困难。因为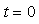 电感电流发生跃变;
电感电流发生跃变;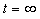 时,
时,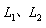 均为短路状态,出现环流,需用磁链守恒或其它方法来确定。而用复频域分析法,就不用考虑这些,它只考虑
均为短路状态,出现环流,需用磁链守恒或其它方法来确定。而用复频域分析法,就不用考虑这些,它只考虑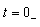 的值。由于电路处于零状态
的值。由于电路处于零状态 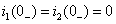 ,故首先作出时域电路的
,故首先作出时域电路的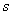 域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。
域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。

S域方法分析线性电路过渡过程的基本步骤
(1)作出时域电路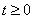 时电路的S域模型。作S域模型时,注意电感和电容元件由于初始状态产生的附加电压源和附加电流源,以及电容电压
时电路的S域模型。作S域模型时,注意电感和电容元件由于初始状态产生的附加电压源和附加电流源,以及电容电压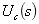 是复频域阻抗
是复频域阻抗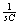 与附加电压源
与附加电压源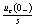 串联支路两端的电压,电感电压
串联支路两端的电压,电感电压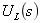 则是复频域阻抗
则是复频域阻抗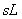 与附加电压源
与附加电压源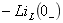 串联支路两端的电压,并要正确标定它们的参考方向。
串联支路两端的电压,并要正确标定它们的参考方向。
(2)根据S域模型,以KVL,KCL和元件的VAR的S域形式为依据,应用等效化简、节点分析法、网孔分析法、叠加定律和戴维南定律应用等基本分析方法进行分析计算,得出待求电量的象函数。
(3)将待求电量的象函数展开为部分分式。
(4)进行拉氏反变换。采用查拉氏反变换表方法,逐项进行反变换为时域原函数,最后解出时域响应。
(一)例题分析
[例题14-1] 拉普拉斯反变换中,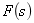 展开为部分分式的计算,下列复频域象函数
展开为部分分式的计算,下列复频域象函数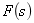 进行拉氏反变换为原函数
进行拉氏反变换为原函数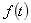 .
.
(1)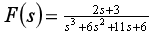 (2)
(2)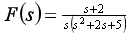 (3)
(3)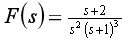
解[解题思路]本题中各复频域象函数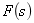 ,都是有理函数,并较为复杂,不能直接查拉氏变换表得出原函数
,都是有理函数,并较为复杂,不能直接查拉氏变换表得出原函数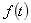 ,需经部分分式展开为简单复频域函数之和,然后逐项查表得出原函数。进行复频域函数
,需经部分分式展开为简单复频域函数之和,然后逐项查表得出原函数。进行复频域函数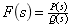 部分分式展开时,第一步将分母多项式
部分分式展开时,第一步将分母多项式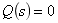 ,求出极点
,求出极点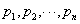 ;第二步,写出
;第二步,写出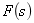 函数含有待定常数
函数含有待定常数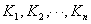 的部分分式;第三步是分别计算出各待定常数;最后,根据线性定律逐项查表得出原函数
的部分分式;第三步是分别计算出各待定常数;最后,根据线性定律逐项查表得出原函数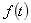 .
.
[解题方法] 1. 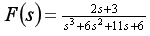
(1)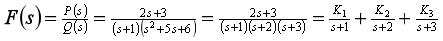
(2)计算待定常数
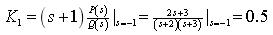
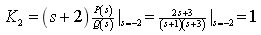
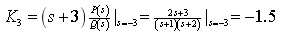
(3)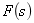 的部分分式为
的部分分式为
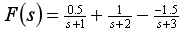
(4)进行拉氏反变换,查拉氏变换表得出
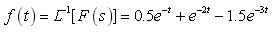
2.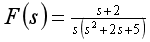
(1)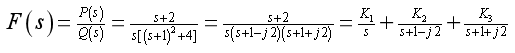
(2)计算各待定常数
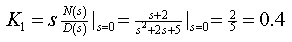

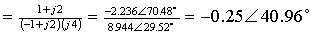
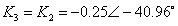
(3)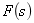 的部分分式为
的部分分式为
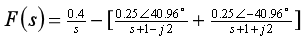
(4)进行拉氏反变换,查拉氏变换表得出
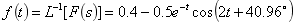
本题反变换中应用的变换式有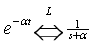
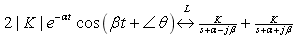
以及欧拉公式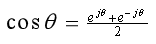
3.
(1)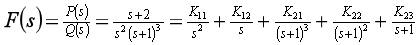
(2)计算各项待定系数
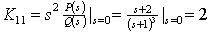
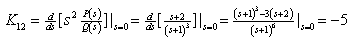
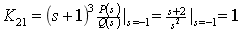
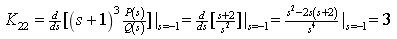
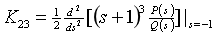
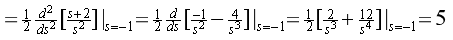
(3)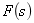 的部分分式为
的部分分式为
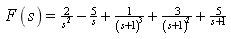
(4)进行拉氏反变换,查拉氏变换表得出
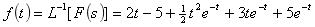
本题计算待定常数时,应用微分公式为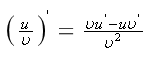
反变换中应用拉氏变换公式有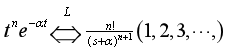
[例14-2] 应用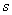 域分析法求一般二阶电路的阶跃响应。如14-2(a)所示电路,求阶跃响应
域分析法求一般二阶电路的阶跃响应。如14-2(a)所示电路,求阶跃响应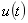 和
和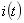 。
。
解: 本题是一般直流二阶电路求阶跃响应,即零状态响应。作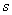 域模型时,初始状态为零,电感元件和电容元件
域模型时,初始状态为零,电感元件和电容元件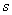 域模型中没有附加电压源。
域模型中没有附加电压源。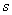 域分析计算的步骤是,首先作出时域电路的
域分析计算的步骤是,首先作出时域电路的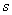 域模型,然后应用节点分析法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应。
域模型,然后应用节点分析法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应。
图14-2
[解题方法] (1)作出时域电路的 域模型如图14-2(
域模型如图14-2( )所示。其电压源电压的象函数是
)所示。其电压源电压的象函数是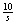 ,复频域感抗
,复频域感抗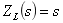 ,复频域容抗
,复频域容抗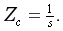
(2)求电压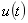 .应用节点分析法,列出节点方程为
.应用节点分析法,列出节点方程为
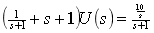 化简得:
化简得: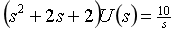
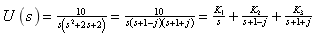
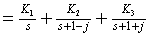
计算待定常数
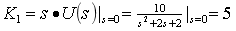
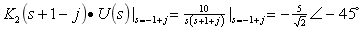
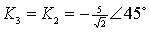
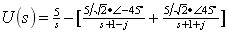
进行拉氏反变换得出
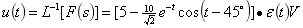
(3)求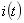
电路的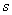 域阻抗为
域阻抗为
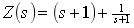
故 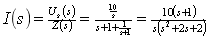
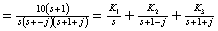
计算待定常数
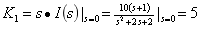
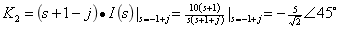
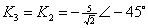

进行拉氏反变换得出
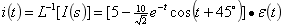 A
A
[例14-3] 激励为指数函数RLC电路的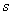 域分析计算。如图14-3(
域分析计算。如图14-3(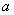 )所示电路,
)所示电路,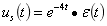 V,
V,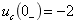 V,
V,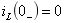 .试用
.试用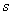 域分析法求电阻元件两端电压
域分析法求电阻元件两端电压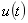 .
.
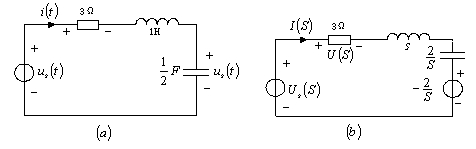
图14-3
[解题思路] 本题是非直流激励二阶电路的分析。分析时关键在于作出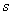 域模型,激励函数查表得出它的象函数,同时要注意电感元件和电容元件由于初始状态产生的附加电压源或附加电流源并正确确定它们的参考方向。作出
域模型,激励函数查表得出它的象函数,同时要注意电感元件和电容元件由于初始状态产生的附加电压源或附加电流源并正确确定它们的参考方向。作出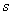 域模型后,按
域模型后,按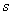 域分析方法的基本步骤进行分析计算得出结果。
域分析方法的基本步骤进行分析计算得出结果。
[解题方法] (1)作出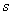 域模型,如图14-3
域模型,如图14-3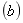 所示。其中电源象函数
所示。其中电源象函数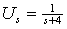 ;由于
;由于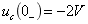 ,故电容元件
,故电容元件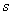 域模型的附加电压源电压为
域模型的附加电压源电压为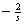 ;又因
;又因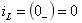 ,故电感元件
,故电感元件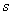 域模型中没附加电压源电压。
域模型中没附加电压源电压。
(2)列KVL方程为 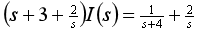
上式等号两边乘s得出 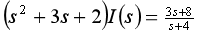
移项得
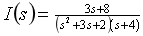
故待求电阻元件两端的电压象函数为
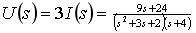
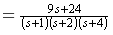
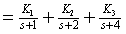
确定各项待定常数
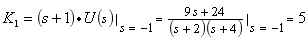
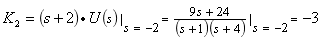
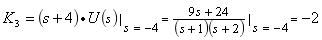
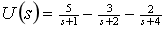
(3)进行拉氏反变换得出
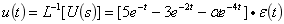 V
V

(二)练习题解答
练习题求下列时间函数的拉氏变换。
(1)
(2)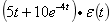
(3)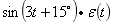
解(1)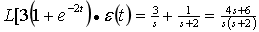
(2)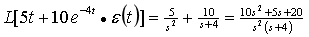
(3)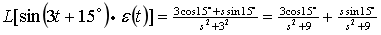
(三)部分习题解答
例14-3.若电路微分方程为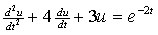 ,且
,且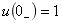 V,
V,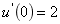
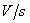 . 求
. 求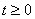 时
时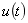 .
.
解 将微分方程进行拉氏变换为
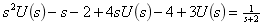
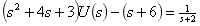
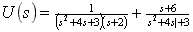

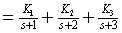
确定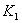 ,
,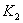 和
和

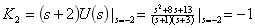
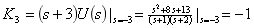
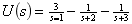
进行拉氏反变换
 V
V 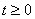
例14-5.如图14-5(a)所示电路,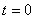 时刻开关K打开,开关动作前电路处于稳态。试用s域分析法求
时刻开关K打开,开关动作前电路处于稳态。试用s域分析法求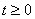 时
时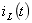 .
.
解 (1)求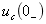 ,
,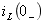 并作
并作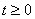 时电路的s域模型。
时电路的s域模型。
由于开关动作前电路处于稳态,则
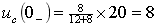 V
V 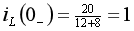 A 故作出
A 故作出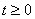 时电路的s域模型,如图14-5(b)所示。
时电路的s域模型,如图14-5(b)所示。
(a) (b)
图14-5
(2)列s域KVL方程为

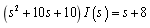
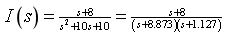
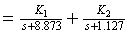
(3)确定常数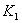 ,
,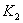
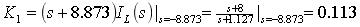
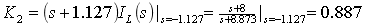
(4)解出电流的s域形式为
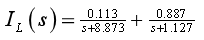
(5)进行拉氏反变换为
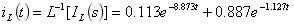 A
A 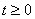
例14-6. 图示电路原处于稳态,t = 0 时开关 S 闭合,试用运算法求解电流 i1(t)。

解:开关闭合之前 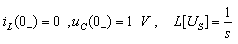 运算电路如图所示,设回路电流为 Ia(s)、Ib(s),方向如图中所示,则有
运算电路如图所示,设回路电流为 Ia(s)、Ib(s),方向如图中所示,则有
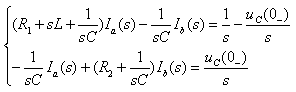
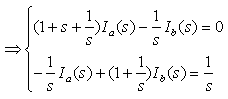
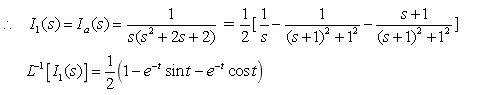
即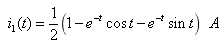
例14-7.下图所示电路中,电路原处于稳态,t=0 时将开关 S 闭合,已知 uS1=2e-2t V, uS2=5V,
R1=R2=5W,L=1H, 求 t ³ 0时的uL(t) 。

解: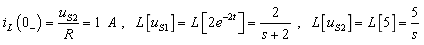 运算电路如右图所示。
运算电路如右图所示。
应用结点法(弥尔曼定理),有
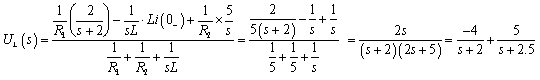
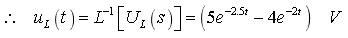
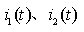 例14-8.求下图所示电路的零状态响应, , 其中,
例14-8.求下图所示电路的零状态响应, , 其中,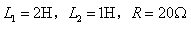
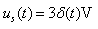 。
。

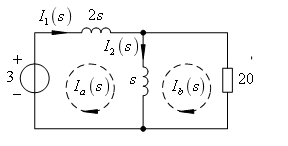
解: 此题若用时域法求解,不论是求初始值,还是求稳态值都比较困难。因为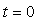 电感电流发生跃变;
电感电流发生跃变;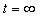 时,
时, 均为短路状态,出现环流,需用磁链守恒或其它方法来确定。而用复频域分析法,就不用考虑这些,它只考虑
均为短路状态,出现环流,需用磁链守恒或其它方法来确定。而用复频域分析法,就不用考虑这些,它只考虑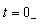 的值。由于电路处于零状态
的值。由于电路处于零状态 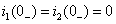 ,复频域电路如右图所示。设网孔电流分别为Ia(s)、Ib(s),方向如图中所示,则网孔电流方程为
,复频域电路如右图所示。设网孔电流分别为Ia(s)、Ib(s),方向如图中所示,则网孔电流方程为
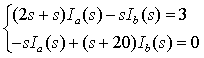 解得
解得 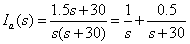
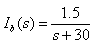
则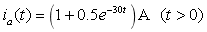
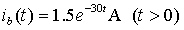
所以 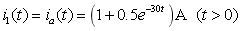
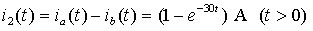
由此可见不论电路有无跃变,也不论电路是否存在稳态环流等,复频域分析法过程完全相同,它不需要列时域的微分方程、也不需考虑时域中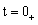 初始值的计算、同时也可以避免时域中确定积分常数而带来的麻烦,它把复杂的时域过渡过程的微积分运算化为复频域的简单的代数运算。这就是复频域分析法的优点。
初始值的计算、同时也可以避免时域中确定积分常数而带来的麻烦,它把复杂的时域过渡过程的微积分运算化为复频域的简单的代数运算。这就是复频域分析法的优点。
![]() 是复频域阻抗
是复频域阻抗![]() 与 串联支路两端的电压,电感电压
与 串联支路两端的电压,电感电压![]() 则是 与附加电压源
则是 与附加电压源![]() 串联支路两端的电压,并要正确标定它们的参考方向。
串联支路两端的电压,并要正确标定它们的参考方向。![]() 域分析法求一般二阶电路的阶跃响应。如14-2(a)所示电路,求阶跃响应
域分析法求一般二阶电路的阶跃响应。如14-2(a)所示电路,求阶跃响应![]() 和
和![]()
![]() 域模型时,初始状态为零,电感元件和电容元件
域模型时,初始状态为零,电感元件和电容元件![]() 域模型中没有附加电压源。然后根据
域模型中没有附加电压源。然后根据![]() 域分析的步骤,首先作出时域电路的
域分析的步骤,首先作出时域电路的![]() 域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。
域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。
![]() 2、求下图所示电路的零状态响应, , 其中,
2、求下图所示电路的零状态响应, , 其中,![]()
![]() 。
。

![]() 电感电流发生跃变;
电感电流发生跃变;![]() 时,
时,![]() 均为短路状态,出现环流,需用磁链守恒或其它方法来确定。而用复频域分析法,就不用考虑这些,它只考虑
均为短路状态,出现环流,需用磁链守恒或其它方法来确定。而用复频域分析法,就不用考虑这些,它只考虑![]() 的值。由于电路处于零状态
的值。由于电路处于零状态 ![]() ,故首先作出时域电路的
,故首先作出时域电路的![]() 域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。
域模型,然后应用上册学过的各种方法法求解出待求量的象函数,并将其展开为部分分式,最后反变换为时域响应即可。