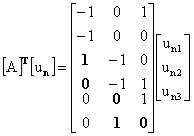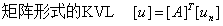关联矩阵
1. 图的矩阵表示(利用电路拓扑图各节点、支路之间的关联性描述矩阵的方法。)
图的矩阵表示是指用矩阵描述图的拓扑性质,即KCL和KVL的矩阵形式。有三种矩阵形式
结点——支路:关联矩阵
回路——支路:回路矩阵
割集——支路:割集矩阵
2. 关联矩阵A(描述结点与支路之间关联性质的一种数学表示方法。)
用矩阵形式描述结点和支路的关联性质。n个结点b条支路的图用n´b的矩阵描述:

注意:每一行对应一个结点,每一列对应一条支路。
矩阵Aa的每一个元素定义为:
l ajk=1 支路 k 与结点 j 关联,方向背离结点;
l ajk= -1 支路 k 与结点 j 关联,方向指向结点;
l ajk =0 支路 k 与结点 j 无关。
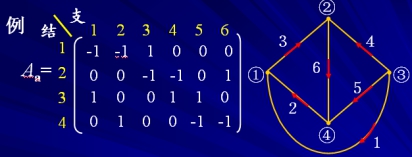
可以看到:
n 每一列只有两个非零元素,一个是+1,一个是-1,Aa的每一列元素之和为零。
n 矩阵中任一行可以从其他n-1行中导出,即只有n-1行是独立的。
降阶关联矩阵A
A的某些列只具有一个+1或一个-1,这样的列对应与划去结点相关联的一条支路。被划去的行对应的结点可以当作参考结点。
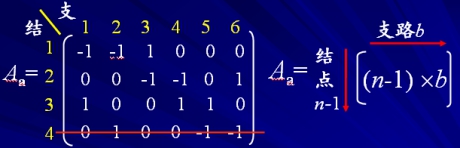
关联矩阵A的作用
l 用关联矩阵A表示矩阵形式的KCL方程;
设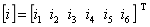 ,以结点④为参考结点
,以结点④为参考结点
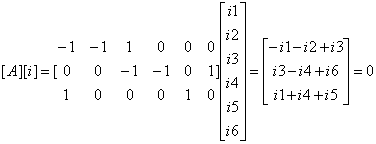
构成n-1个独立方程,矩阵形式的KCL: [ A ][ i ]= 0
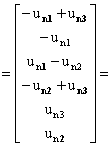
l 用矩阵[A]T表示矩阵形式的KVL方程。
设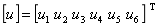 ,
,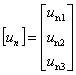
则: