18.5  分段线性化方法

    分段线性化方法(也称折线法)是研究非线性电路的一种有效的方法。它的特点在于能把非线性特性曲线用一些分段的直线来近似地逼近，对于每个线段来说，又可应用线性电路的计算方法。

非线性电阻的特性曲线，用分段线性化来描述。例如图17.9所示p-n结二极管的特性曲线，该曲线可以粗略地用两段直线来描述，如图中粗线A0B。这样，当这个二极管施加正向电压时，它相当于一个线性电阻，

其电压、电流关系用直线0B表示；当电压反向时，二极管截止，电流为零，它相当于电阻值为∞的电阻，其电压、电流关系用直线A0表示。

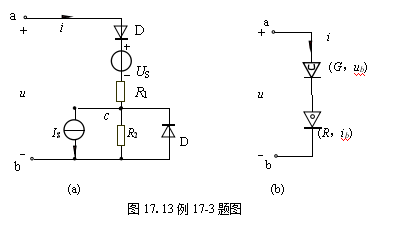
 理想二极管的电压、电流关系可由负u轴和正i轴这样的两条直线线段组成。理想二极管的符号及其特性曲线如图(b)所示。理想二极管的特性是：若电压u > 0(正向偏置)时，则理想二极管工作在电阻为0的线性区域；若u < 0（反向偏置）时，则其工作在电阻为∞的线性区域。分析理想二极管电路的关键，在于确定理想二极管是正向偏置（导通），还是反向偏置（截止）。如果属于前一种情况，二极管以短路线替代，若属于后一种情况，则二极管以开路替代，替代后都可以得到一个线性电路，容易求得结果。电路中仅含一个理想二极管时，利用戴维宁定理分析计算十分方便，毋需使用图解方法。

    在分段线性描述中，凹电阻元件和凸电阻元件是两个理想的分段线性模型。下面简单介绍。

凹电阻元件（Concave  resistor）是一个分段电压控制电阻元件，其特性曲线如

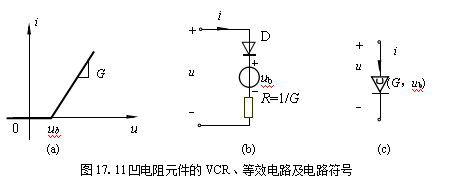
图17.11(a)所示，G表示图示线性区段的斜率，u_b表示折点电压。凹电阻元件的特性方程为

                                           (17-8)

由式(17-8)凹电阻特性方程和图13.11(a)特性曲线可知

 当 u < u_b时，i = 0；

 当 u > u_b时，。

凹电阻元件可由一个理想二极管与电压为u_b的电压源和电导为G的电阻相互串联的电路来实现，如图17.11(b)所示，其电路符号如图17.11(c)所示。

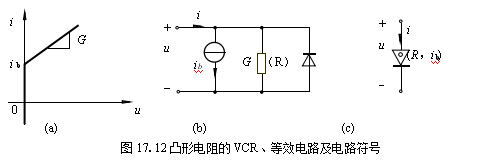
凸电阻元件(Convex resistor)是分段线性电流控制电阻元件，该元件可用线性区段的斜率G和折点电流i_b，两个参数来描述。其特性曲线如图13.12(a)所示。凸电阻元件的方程为

                                            (17-9)

由式(17-9)特性方程及图17.12(a)特性曲线可知：当i < i_b 时，u = 0，当 i > i_b 时，，凸电阻元件的等效电路如图17.12(b)所示,它可用一个电流等于i_b的电流源与电导等于G的电阻和理想二极管并联组合来表示。凸电阻元件的电路符号如图17.11(c)所示。

 分段线性化处理中，隧道二极管的特性曲线可近似如图17.15(a)所示，可分1、2、3三个区域三段直线段来表示。每个直线段的斜率分别为G_a、G_b和G_c。而这三段直线可分

解为如图(b)中直线AOB，折线OCD和折线OEF，这3条曲线分别代表了电导为G₁的线性电阻、折点为u_b1而斜率为G₂的凹电阻和折点为u_b2而斜率为G₃的凹电阻的特性曲线，所以图17.15(a)的隧道二极管的特性曲线是其等效电路如17.16图三个元件的并联的特性曲线。

为了使上述等效电路输入端口的电压、电流关系与隧道二极管的分段线性近似电压、电流关系完全相符，图17.15中的三个参数必须满足下列关系：

                             在区域1中

                         在区域2中

和                                       在区域3中

从而得

和                             

上述等效电路的各支路的电流可分别用函数式表示为

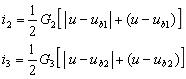
根据KCL可得

另外，隧道二极管或非线性电阻分段线性化后，每个区域也可用等效无源或有源线性一端口电路表示。这里不在赘述，请读者自行分析。

隧道二极管的静态工作点可以用图解的方法确定。但要注意，如果静态工作点位于图17.17(a)所示位置，表示Q₁、Q₂、Q₃确实是工作点。如果负载线与分段区域线段的特性交点如图17.17(b)所示位置，则只有Q₃为实际的工作点，而Q₁和Q₂并不是实际工作点，而是虚点。

例17-2  求如图17.10所示电路中理想二极管通过的电流。

解  在分析理想二极管电路时，首先确定二极管是否导通。当这个二极管接在复杂的电路中时，可以先把含二极管的支路断开，利用戴维宁定理求得电路其余部分的戴维宁等效电路后，再把含二极管的支路接上，然后在这个简单的电路中，确定二极管工作区域，且判断它是否导通。

在图17.10(a)所示的电路中除去二极管支路以外，由电路的其余部分，可求得其等效电路的电压Uoc和电阻Req为

该等效电路如图17.10(b)所示，由此可得，二极管两端的电压，它处于截止状态，因此二极管不能导通，电流。

 例17-3  如图13.13所示电路，R₁ = 1Ω，R₂ = 2Ω，U_S = 1V，I_S = 1A，D为理想二极管，求在平面上画出此特性曲线。

  解  图17.13(a)所示电路，可视为图(b)所示的一个凹形电阻与一个凸形电阻相串联电

路。二者的特性曲线分别如图13.14(a)和(b)所示。

在图17.14(a)中，当 时，，u_ac > 0；i = 0时，u_ac<0。

    在图17.14(b)中，当i > I_S时， ；i < i_s时，。两个非线性电阻串联后的特性曲线如图17.14(c)所示。