
耦合电感的并联去耦等效
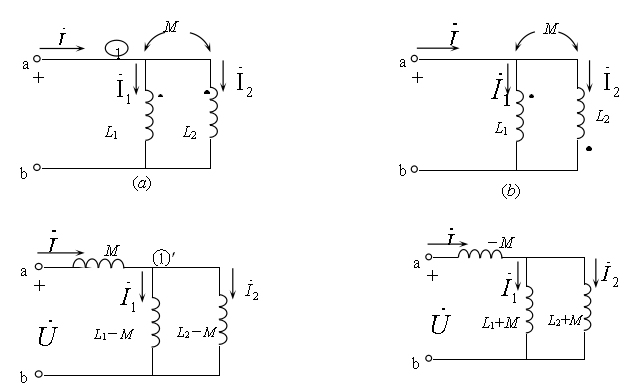
互感线圈的并联也有两种形式,一种是两个线圈的同名端相连,称为同侧并联,如图10.16(a)所示;另一种是两个线圈的异名端相连,称为异侧并联。如图10.16(b)。在正弦稳态情况下对同侧并联,列电路方程:
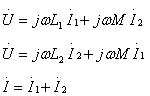 (10.8)
(10.8)
由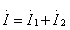 可得
可得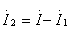 ,
,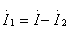 再分别代入第1条支路和第2条支路方程中,则有:
再分别代入第1条支路和第2条支路方程中,则有:
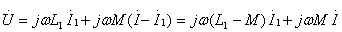
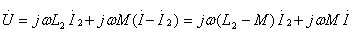 (10.9)
(10.9)
根据式(10.9)的伏安关系及等效的概念,图10.16(a)所示的具有互感的电路就可以用图10.16(c)所示无互感的电路来等效。
 (c) (d)
(c) (d)
图10.16 互感线圈的并联及去耦等效电路
同理,对异侧并联图10.16(b)也可以得到无互感的等效电路如图10.16(d)。象这样把具有互感的电路化为等效的无互感的电路的处理方法,称为去耦法,把得到的等效的无互感电路称为去耦等效电路。等效电感与电流的参考方向无关。去耦等效电路中的结点,如图10.16(c)中的①′,不是图10.16(a)原电路的结点①,原结点移至 的前面
的前面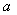 点。由图10.16(c)可直接求出两个互感线圈同侧并联时的等效电感为:
点。由图10.16(c)可直接求出两个互感线圈同侧并联时的等效电感为:

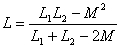
由图10.16(d)可直接求出两互感线圈异侧并联时的等效电感为:
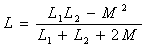
2 耦合电感的T形等效
如果耦合电感的2条支路各有一端与第三条支路形成一个仅含三条支路的共同结点,称为耦合电感的T形联接。显然耦合电感的并联也属于T形联接。T形连接有两种方式,同名端为共同端的T形连接和异名端为共同端的T形连接。
一种是同名端连在一起的如图10.17(a)称为同名端为共同端的T形连接;另一种是异名端连在一起的如图10.17(b)称为异名端为共同端的T形连接。
对图10.17(a)同名端为共同端相连的电路,其电压方程为
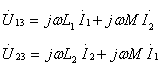 (10.10)
(10.10)
由KCL 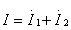 得
得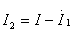
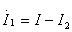 代入式(10.10)变换后,得:
代入式(10.10)变换后,得:
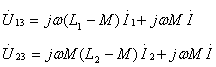 (10.11)
(10.11)
由式(10.11)可得图10.17(a)的去耦等效电路为图10.17(c)。
同理,两互感线圈异名端为共端的电路图10.17(b)的去耦等效电路为图10.17(d)。
上述分别对具有耦合电感的串联、并联及T型电路进行分析,得到了相应的去耦等效电路。在去耦等效电路中采用无互感电路进行分析和计算,但要注意等效的含义。
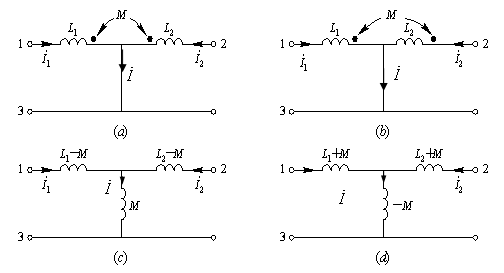
图10.17 互感线圈的T型连接及去耦等效电路
