-
1 电子教材
-
2 PPT
首先看一下如何测试一个两位数加法计算器的程序。
测试需求:测试两个参数的值相加后的结果是否正确。其中:
Ø 输入的数值在-99到99之间。
Ø 大于99或小于-99的输入应被拒绝,并显示错误信息。
根据测试需求开始测试。分别给第1个参数和第2个参数输入表中的值,得到的测试结果如表6-1所示。
表6-1 测试数据的结果
第1个参数的值 | 第2个参数的值 | 两数相加后的值 |
| 1 | 1 | 2 |
| 1 | 2 | 3 |
| 1 | -1 | 0 |
| 1 | -2 | -1 |
| ... | .. | ... |
很明显,如果对第一个参数的值分别取从-99到99的199个数,第2个参数的值分别取从-99到99的199个数,我们不可能对两位数相加的所有情况进行穷举测试。如果不能进行穷举测试,则将面临以下问题:
Ø 在测试了1+1、1+2、1+ (-1)和1+(-2)之后,还是否有必要测试1+3和1+4?
Ø 如果不对加法计算器程序进行穷举测试,能否放心地认为所有的参数组合都是正确的?
对以上两个问题,能否找到解决的办法?
在运用等价类技术解决上述问题之前,首先来看看什么是等价类划分法。
等价类划分设计方法是把所有可能的输入数据,即程序的输入数据集合划分成若干个子集(即等价类),然后从每一个等价类中选取少数具有代表性的数据作为测试用例数据。
接下来具体看看如何运用等价类技术解决上述问题。
(1)在本案例中我们根据测试需求可以把两位数加法分为如图2-1所示的3个等价类:一个有效数据的等价类,两个无效数据等价类(有效数据等价类就是由那些对程序的规格说明有意义的、合理的输入数据所构成的集合;无效数据等价类就是那些对程序的规格说明不合理的或无意义的输入数据所构成的集合)。
(2)在实际工作中,通常在确立了等价类以后,把程序中的所有等价类建立为等价类表,以便在设计测试用例时有所依据(表2-2)。

图6-1 等价类划分
表6-2 等价类表
| 序号 | 功能项 | 有效等价类 | 编号 | 无效等价类 | 编号 |
| 1 | 两位数加法 | -99<=加数取值<=99 | 2 | 加数取值<-99 加数取值>99 | 1 3 |
| 2 | … | … | … | … | …… |
(3)根据上面的等价类表,就可以确定测试用例,步骤如下:
1)为等价类表中的每一个等价类分配一个唯一的编号。
2)设计一个新的测试用例,使它能够尽量覆盖尚未覆盖的有效等价类。重复这一步骤,从而使所有有效等价类均被测试用例所覆盖(表6-3)。
3)与步骤2)类似,设计一个新的测试用例,使它只覆盖一个无效等价类。重复这一步骤,从而使所有无效等价类均被测试用例所覆盖(表6-3)。
表6-3 测试用例列表
| 测试用例编号 | 输入数值 | 所属等价类 | 预期输出 |
| 1 | -50+24 | 2 | 正确输出:-26 |
| 2 | -130 | 1 | 错误信息 |
| 3 | 125 | 3 | 错误信息 |
(4)细化等价类划分
在测试“-99<=数值<=99”的这个等价类区间的时候,会发现如10+40、-20+30和-30+ (-30)这类的正数相加,正数负数相加,负数相加也是不同的等价区间。因此可以使用更多的等价类划分(图6-2)。
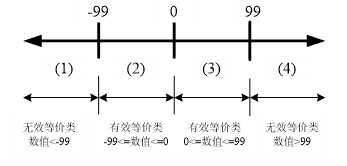
图6-2 有效等价类细化
根据以上等价类划分的结果,得出表6-4所示的等价类表。
表6-4 等价类表
| 序号 | 功能项 | 有效等价类 | 编号 | 无效等价类 | 编号 |
| 1 | 两位数加法 | -99≤加数取值≤0 0≤加数取值≤99 | 2 3 | 加数取值<-99 加数取值>99 | 1 4 |
根据上面划分的4个等价类可知,至少需要5个测试用例(表6-5)。
表6-5 测试用例
| 测试用例编号 | 输入数值 | 所属等价类 | 预期输出 |
| 1 | 50+2 | 3 | 正确输出:52 |
| 2 | -63+(-20 | 2 | 正确输出:-83 |
| 3 | -30+10 | 2,3 | 正确输出:-20 |
| 4 | -130 | 1 | 错误信息 |
| 5 | 125 | 4 | 错误信息 |


