地理空间的数学基础主要包括地球空间参考、空间数据投影及坐标转换、空间尺度及地理格网。

地球空间参考解决地球的空间定位与数学描述问题，空间数据投影及坐标转换主要解决如何把地球曲面信息展布到二维平面，空间尺度规定在多大的详尽程度研究空间信息，地理格网在于建立组织空间信息空间区域框架方法，实现空间数据的科学有效的管理。因此，掌握地理空间的数学基础是正确应用GIS 完成各种空间分析与应用的基础。

众所周知，地球是一个近似球体，其自然表面是一个极其复杂的不规则曲面。

为了深入研究地理空间，就有必要建立地球表面的几何模型。根据大地测量学的研究成果，地球表面的几何模型可以分为四类：

第一类是地球的自然表面，它是一个起伏不平，十分不规则的表面，包括海洋底部、高山高原在内的固体地球表面；

第二类是相对抽象的面，即大地水准面。它是假设当海水处于完全静止的平衡状态时，从海平面延伸到所有大陆下部，而与地球重力方向处处正交的一个连续、闭合的水准面。水准面是一个重力等位面。对于地球空间而言，存在无数个水准面，大地水准面是其中一个特殊的重力等位面，它在理论上与静止海平面重合。大地水准面包围的形体是一个水准椭球，称为大地体。

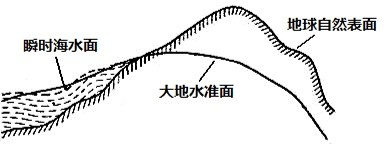
尽管大地水准面比起实际的固体地球表面要平滑得多，但实际上由于地质条件等因素的影响，大地水准面存在局部的不规则起伏，并不是一个严格的数学曲面，因而在大地测量和GIS 应用中仍然存在极大的困难。因此，就有第三类地球表面的几何模型：地球椭球面。

总体上讲，大地体非常接近旋转椭球，而后者的表面是一个规则的数学曲面。所以在大地测量以及GIS 应用中，一般都选择一个旋转椭球作为地球理想的模型，称为地球椭球。

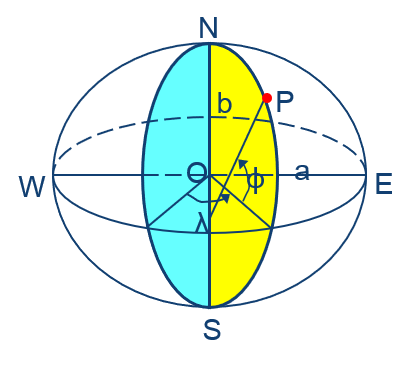
在有关投影和坐标系统的叙述内容中，地球椭球有时也常被称为参考椭球。

最后一类地球表面几何模型是数学模型，它是在解决其它一些大地测量学问题时提出来的，如类地形面、准大地水准面、静态水平衡椭球体等。不同的限制条件，不同的研究方法，得到的地球椭球不尽相同。目前国际上使用的地球椭球种类繁多，如：克拉索夫斯基、海福特、WGS-84等等。

有了参考椭球，再指定一个大地基准面，将这个椭球体与大地体联系起来，就可以建立地理空间坐标系统了。地理空间坐标系统提供了确定空间位置的参照基准。根据表达方式的不同，地理空间坐标系统通常分为球面坐标系统和平面坐标系统。平面坐标系统也常被成为投影坐标系统。