地面点虽然可以沿法线表示到参考椭球面上，但是用缩小的球面，如地球仪，不便于使用和保管，一般均使用平面图。

参考椭球面是不可展曲面，不可能用物理的方法将它展成平面。因为那样必然会使曲面产生裂口、皱褶和重叠。因此，要把参考椭球面上的点、线、面换算到平面上，就要解决曲面到平面的矛盾。为了解决这一问题，地图投影就应运而生。

在数学中，投影（Project）的含义是指建立两个点集之间一一对应的映射关系。同样，在地图学中，地图投影的实质就是按照一定的数学法则，将地球椭球面上的经纬网转换到平面上，建立地面点位的地理坐标与地图上相对应的平面直角坐标之间一一对应的函数关系。

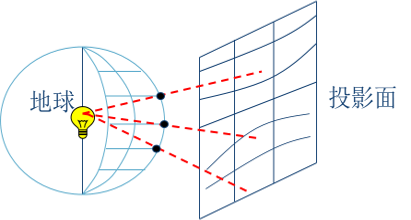
由于地球表面是一个不规则的曲面,即使把它当作一个椭球体或正球体表面,在数学上讲,它也是一种不可能展开的曲面，要把这样一个曲面表现到平面上,就会发生裂隙或褶皱。因此，为了形成一幅完整的地图，在投影面上，就需要运用经纬线的“拉伸”或“压缩”来避免,这样一来,投影地图也就因此而产生了变形。为了正确使用地图，就必须了解投影后产生的变形。

根据地面事物几何特性的变形情况，地图投影的变形通常可分为长度、面积和角度三种变形，并通过它们的变形比来衡量投影变形。

投影后地图上的经纬线长度与椭球体上经纬线的长度并不完全相同，地图上的经纬线长度也并不都是按照同一比例缩小的，这表明地图上具有长度变形。如果地图上经纬线网格面积不是按照同一比例缩小就会产生面积变形，面积变形的原因与长度变形直接相关。投影面上任意两方向线所夹之角与原球面上相应的角度之间存在差异，就产生了角度变形。控制投影各种变形，满足具体应用的需求，是建立地图投影需要考虑基本问题。

在历史上，众多的数学家、物理学家、天文学家等创立了种类繁多的地图投影。这对这些种类繁多的地图投影，国内外学者提出了许多地图投影的分类方案。但迄今尚无一种分类方案能被一致认同。通常采用以下两种分类方法：一种是按地图投影的构成方法分类，另一种是按地图投影的变形性质分类。

按地图投影的构成方法，地图投影可分为：几何投影和非几何投影。几何投影是把椭球面上的经纬线网投影到几何面上，然后将面展平面得到。根据使用辅助投影面的类型，几何投影又可划分为：方位投影、圆柱投影、圆锥投影。

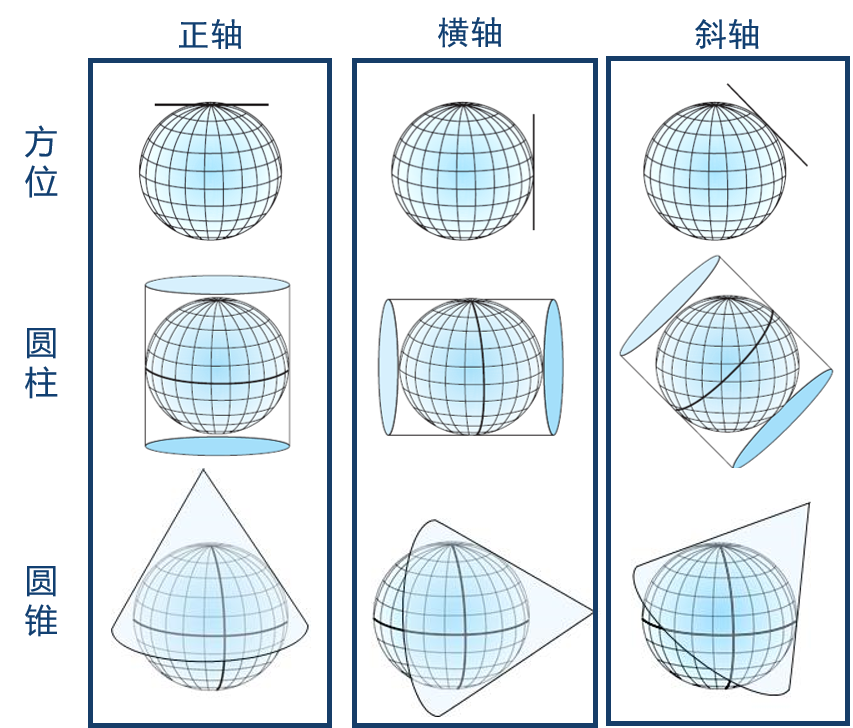
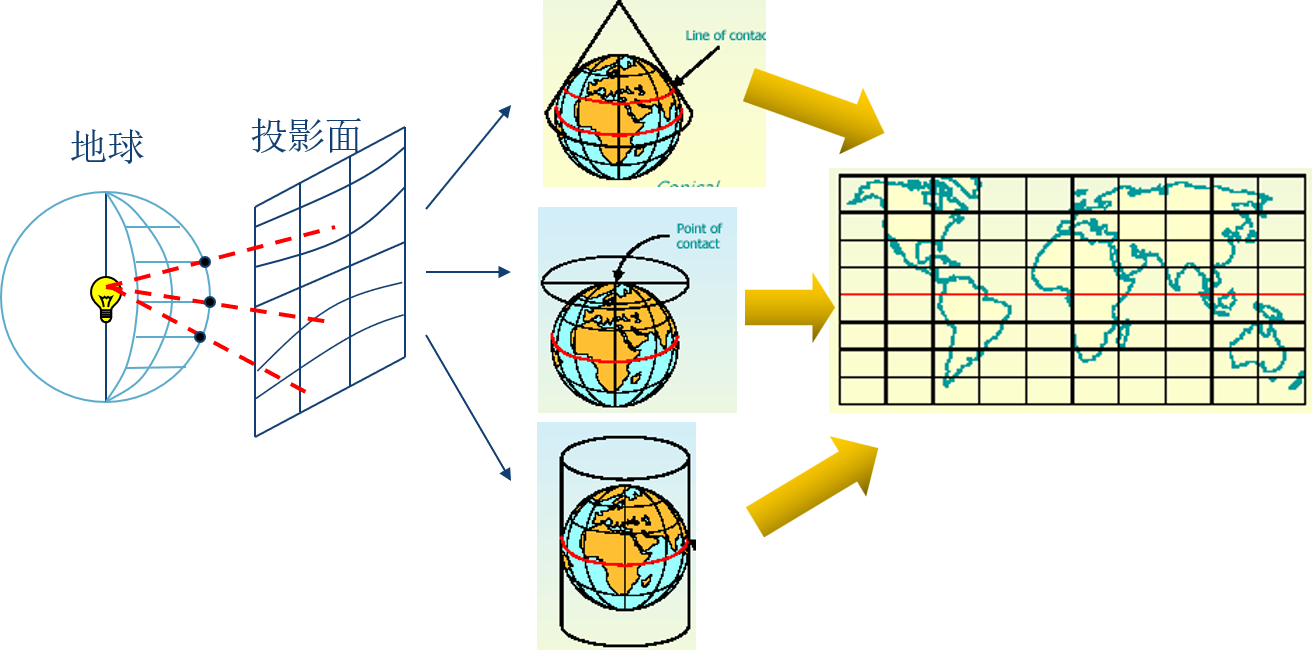根据投影面与地球自转轴间的方位关系，几何投影又可划分为：正轴投影、横轴投影、斜轴投影。而根据投影面与地球的位置关系，几何投影又可划分为：割投影和切投影。

相对于几何投影，非几何投影不是借助几何面，而是根据某些条件，用数学解析法确定球面与平面之间，点与点的函数关系。在这类投影中，一般按经纬线形状可分为伪方位投影、伪圆柱投影、伪圆锥投影和多圆锥投影几类：

在伪方位投影中：纬线为同心圆，中央经线为直线，其余的经线均为对称于中央经线的曲线，且相交于纬线的共同圆心。

在伪圆柱投影中：纬线为平行直线，中央经线为直线，其余的经线均为对称于中央经线的曲线。

在伪圆锥投影中：纬线为同心圆弧，中央经线为直线，其余经线均为对称于中央经线的曲线。

在多圆锥投影中：纬线为同周圆弧，其圆心均位于中央经线上，中央经线为直线，其余的经线均为对称于中央经线的曲线。

按投影变形性质进行分类，地图投影可以分为等角投影、等面积投影和任意投影和等距投影：等角投影是指投影前后，对应的微分面积保持图形相似，又称作正形投影。等面积投影是指在投影平面上任意一块面积与椭球面上相应的面积相等，面积变形等于零。而任意投影和等距投影则是指任意投影，长度、面积和角度都有变形，它既不等角又不等面积，可能还存在长度变形。

圆锥投影、方位投影、圆柱投影，均可按其变形性质分为等角投影、等面积投影和任意投影。伪圆锥和伪圆柱投影中有等面积投影和任意投影，而都以等面积投影较多。

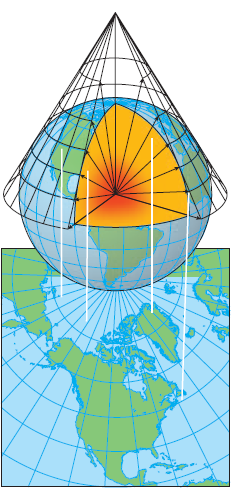
常用的地图投影主要有三类：高斯—克吕格投影、通用横轴墨卡托投影和兰勃特等角投影在投影分类中，高斯—克吕格投影是横轴等角切圆柱投影。该投影的变形特征是：在同一条经线上，长度变形随纬度的降低而增大，在赤道处为最大；在同一条纬线上，长度变形随经差的增加而增大，且增大速度较快。

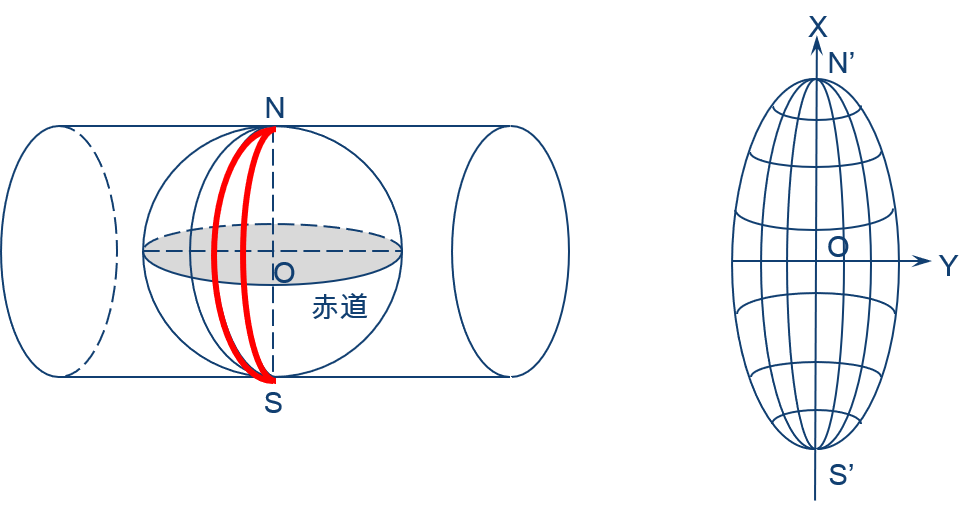
我国规定1:1 万、1:2.5 万、1:5 万、1:10 万、1:25 万、1:50 万比例尺地形图，均采用高斯投影。1:2.5万 至1:50 万比例尺地形图采用经差6˚分带，1:1 万比例尺地形图采用经差3˚分带。

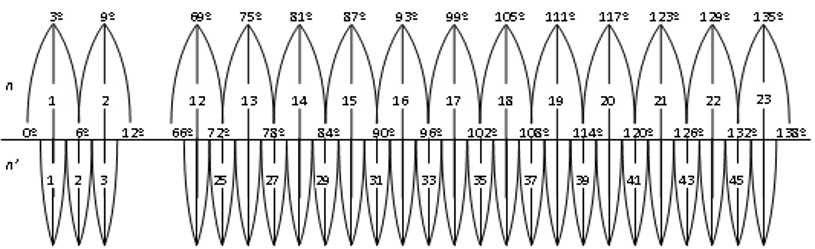
高斯投影是具有国际性的一种地图投影，适合于幅员广大的国家或地区，它按经线分带进行投影，各带坐标系、经纬网形状、投影公式及变形情况都是相同的，利于全球地图拼接。

通用横轴墨卡托投影是一种横割圆柱等角投影，圆柱面在北半球84度和南半球84度处与椭球体相割，它与高斯—克吕格投影十分相似，也采用在地球表面按经度每6˚分带。其带号是自西经180˚由西向东每隔6˚一个编号。兰勃特等角投影在双标准纬线下是“正轴等角割圆锥投影”。常用的墨卡托(Mercator)投影是它的一个特例。

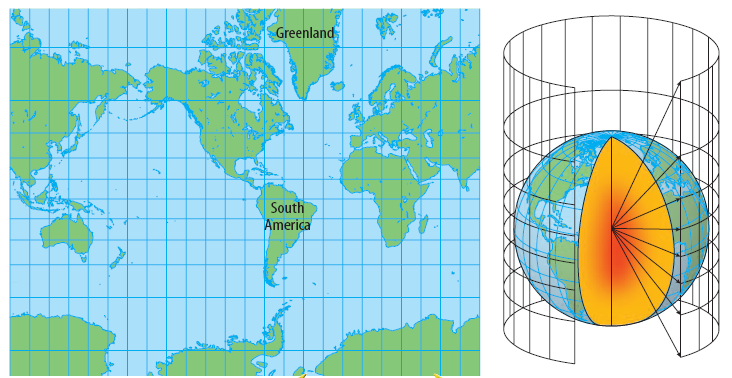
地图投影选择得是否恰当，直接影响着地图的精度和使用价值。选择制图投影时，主要考虑以下因素：制图区域的范围、形状和地理位置，地图的用途、出版方式及其他特殊要求等，其中制图区域的范围、形状和地理位置是主要因素。