空间数据结构是指对空间数据逻辑模型描述的数据组织关系和编排方式的具体实现，是空间数据逻辑模型与数据文件格式间的桥梁。它对地理信息系统中数据存储、查询检索和应用分析等操作处理的效率有着至关重要的影响。空间数据结构是地理信息系统沟通信息的桥梁，只有充分理解地理信息系统所采用的特定数据结构，才能正确有效地使用系统。

在地理信息系统中，较常用的有栅格数据结构和矢量数据结构，除此之外还有混合数据结构、镶嵌数据结构和多维数据结构等。

矢量数据结构直接以几何空间坐标为基础，通过记录采样点坐标，尽可能精确地表示点、线、面等地理实体。因此，通过这种数据组织方式，可以得到精美的地图；另外，矢量结构还可以对复杂数据以最小的数据冗余进行存贮。它具有数据精度高，存储空间小等特点，是一种高效的图形数据结构。

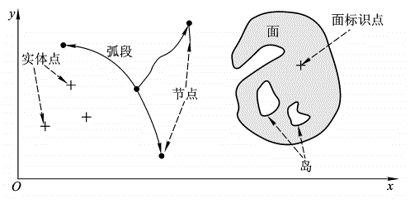
在矢量数据结构中，传统的组织方法是几何图形及其关系用文件方式组织，而属性数据通常采用关系型表文件记录，两者通过实体标识符连接。矢量数据结构按其是否明确表示地理实体间的空间关系分为实体数据结构和拓扑数据结构两大类。

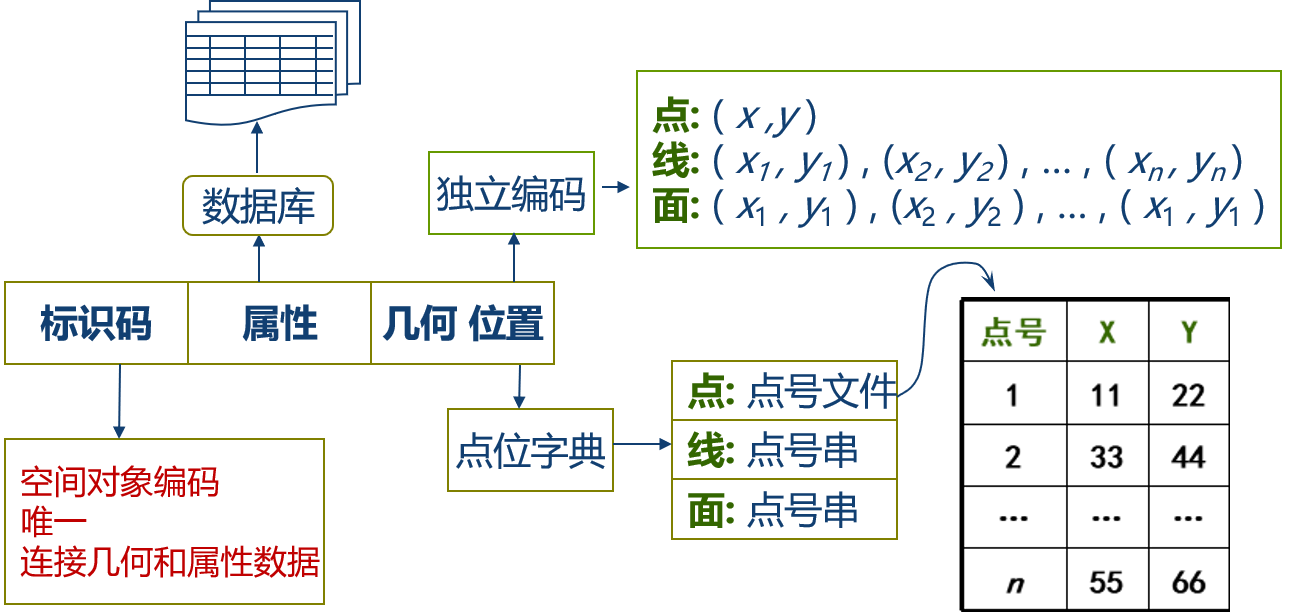
实体数据结构也称spaghetti [spə'ɡeti]数据结构，是指构成多边形边界的各个线段，以多边形为单元进行组织。按照这种数据结构，边界坐标数据和多边形单元实体一一对应，各个多边形边界点都单独编码并记录坐标。如图所示的多边形A、B、C、D，可以采用两种结构分别组织。

第一种结构：

第二种结构：

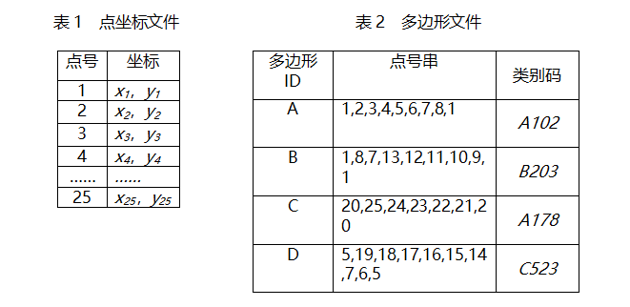
实体数据结构具有编码容易、数字化操作简单和数据编排直观等优点；但也有以下明显缺点：

一是相邻多边形的公共边界要数字化两遍，造成数据冗余存储，可能导致输出的公共边界出现间隙或重叠；

二是缺少多边形的邻域信息和图形的拓扑关系；

三是岛只作为一个单个图形，没有建立与外界多边形的联系。

因此，实体式数据结构只适用于简单的系统，如计算机地图制图系统。如果要建立点与边，边与面之间的关系，就需要为空间数据构建拓扑关系。

拓扑(topology)关系是一种对空间结构关系进行明确定义的数学方法。具有拓扑关系的矢量数据结构就是拓扑数据结构。拓扑数据结构是GIS 分析和应用功能所必需的。拓扑数据结构没有固定的格式，还没有形成统一标准，但基本原理相同的。它们的共同的特点是：点是相互独立的，点连成线，线构成面。每条线始于起始结点，止于终止结点，并与左右多边形相邻接。

拓扑数据结构最重要的特征是具有拓扑编辑功能；这种拓扑编辑功能，不但能够对数字化原始数据进行自动差错编辑，而且可以自动形成封闭的多边形边界，为由各个单独存储的弧段组成的各类多边形及建立空间数据库奠定基础。

目前常用的拓扑数据结构有：索引式、双重独立编码结构、链状双重独立编码结构等。

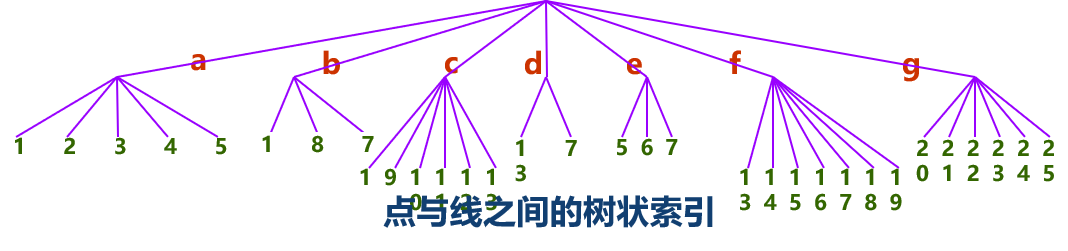
索引式数据结构采用树状索引，以减少数据冗余并间接增加邻域信息，具体方法是：先对所有边界点进行数字化，将坐标对以顺序方式存储，再由点索引与边界线号相联系，以线索引与各多边形相联系，形成树状索引结构。因此，建立这样的索引式拓扑结构需要3 个表文件，第一个记录多边形和边界弧段的关系，第二个记录边界弧段由哪些点组成；第三个文件记录每个顶点的坐标，他们之间通过索引号进行链接。这样的树状索引结构消除了相邻多边形边界的数据冗余和不一致的问题，在简化过于复杂的边界线或合并多边形时可不必改造索引表，邻域信息和岛状信息也可以通过对多边形文件的线索引处理得到。但是过程比较繁琐，因而给邻域函数运算、消除无用边、处理岛状信息以及检查拓扑关系等带来一定的困难，而且两个编码表都要以人工方式建立，工作量大且容易出错。

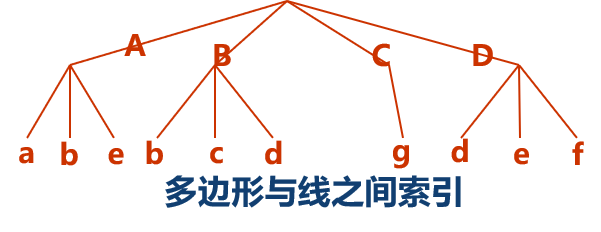
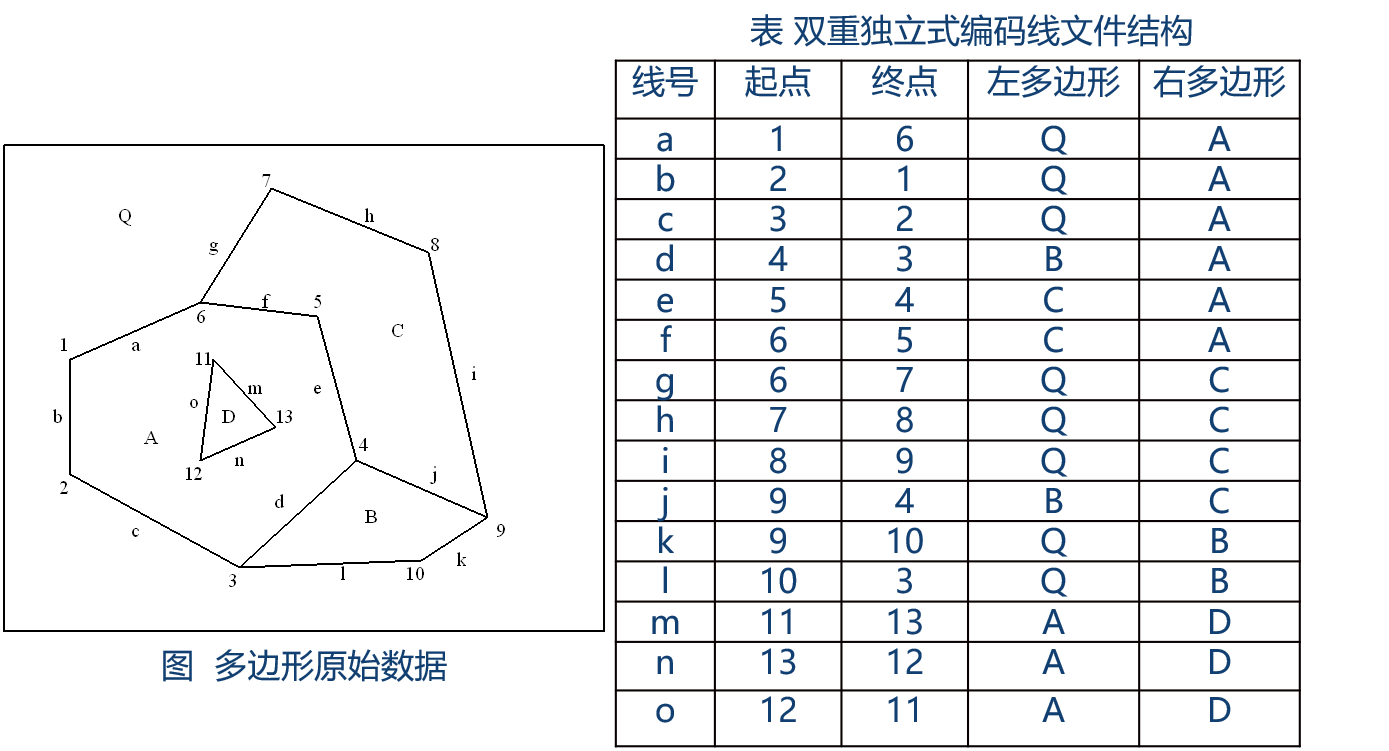
第二种常用的拓扑结构是双重独立编码结构。双重独立编码结构最早是美国人口统计系统采用的一种编码方式，简称DIME（Dual Independent Map Encoding）编码系统，双重独立编码结构是以城市街道为编码主体，对图上网状或面状要素的任何一条线段，用顺序的两点定义以及相邻多边形来予以定义。

在这种数据结构中，结点与结点，或者多边形与多边形之间为邻接关系，结点与线段，或者多边形与线段之间为关联关系。利用这种拓扑关系可以有效地进行数据存储正确性检查，如多边形是否封闭等，同时，也便于对数据进行更新和检索。

除线段拓扑关系文件外，双重独立编码结构还需要点文件和面文件，其结构与索引结构的点表和面表相同。

由于DIME是以城市街道为编码主体，因此，这种编码结构尤其适用于城市地籍宗地的管理。在宗地管理中，界址点对应于点、界址边对应于线段，而面对应于多边形，各种要素都有惟一的标识符。DIME在城市信息系统发挥了重要作用，然而，由于在DIME中，一条边只能用直线两端点的序号及相邻的多边形来表示，而对弧段的中间点没有存储。这对实际应用带来了一定的困扰。因此，有人针对这个问题，对DIME数据结构进行了改进，这就是链状双重独立式数据结构。

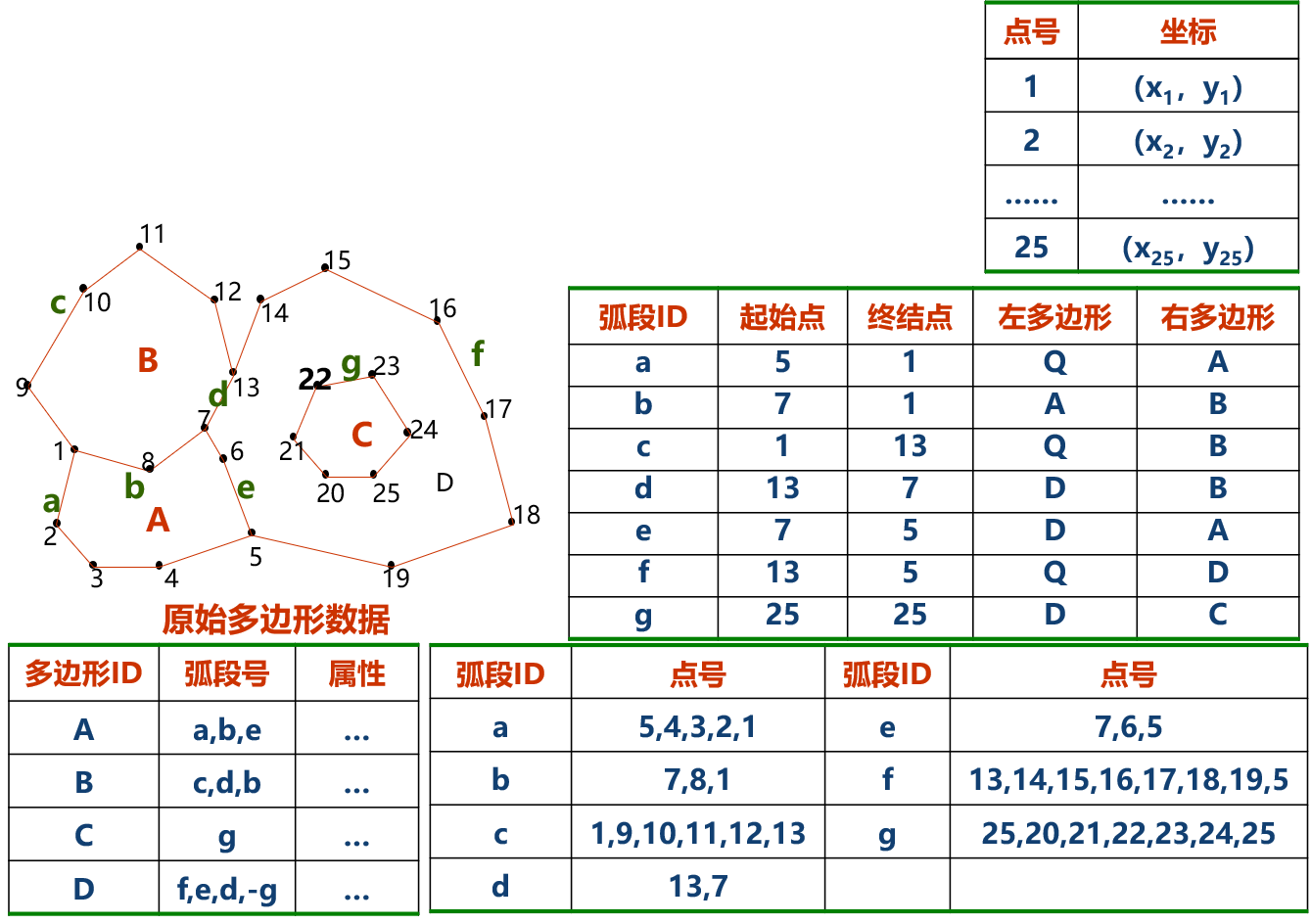
在这种链状数据结构中，将若干直线段合为一个弧段（或链段），每个弧段可以有许多中间点。因此，相对于DIME，链状双重独立数据结构主要有四个文件，分别是：多边形文件、弧段文件、弧段点文件和点坐标文件。多边形文件主要由多边形记录组成，包括多边形号、组成多边形的弧段号，以及周长、面积、中心点坐标及有关“洞”的信息等，多边形文件也可以通过软件自动检索各有关弧段生成，并同时计算出多边形的周长和面积以及中心点的坐标，当多边形中含有“洞”时，则此“洞”的面积为负，并在总面积中减去，其组成的弧段号前也冠以负号；弧段文件主要由弧记录组成，存储弧段的起止结点号和弧段左右多边形号；弧段坐标文件由一系列点的位置坐标组成，一般从数字化过程获取，数字化的顺序确定了这条链段的方向。结点文件由结点记录组成，存储每个结点的结点号、结点坐标及与该结点连接的弧段。结点文件一般通过软件自动生成，因为在数字化的过程中，由于数字化操作的误差，各弧段在同一结点处的坐标不可能完全一致，需要进行匹配处理。当其偏差在允许范围内时，可取同名结点的坐标平均值。如果偏差过大，则弧段需要重新数字化。

国际著名GIS软件平台开发商美国ESRI公司的ARCGIS产品中的COVERAGE数据模型就是采用链状双重独立编码数据结构。

矢量数据结构中还有一种结构就是网络数据结构。网络数据结构是由一组相连的边和交汇点,以及连通性规则组成，用于表示现实世界中的网状线性系统。网络数据结构是GIS数据建模和空间分析所必须的一种常用数据结构。采用网络结构进行建模的常见实体包括:交通网络系统、电力系统、地下管网系统和河网系统等。

在GIS网络建模中，根据网络是否记录位置特征可以将其分为：几何网络和逻辑网络，几何网络主要强调边和节点的空间位置关系；逻辑网络则强调边与边之间的拓扑关系。在实际建模与存储时，由于分析需要，一般会同时考虑位置关系和拓扑关系。如果在网络数据结构中定义了每条边的方向，则为有向网络。

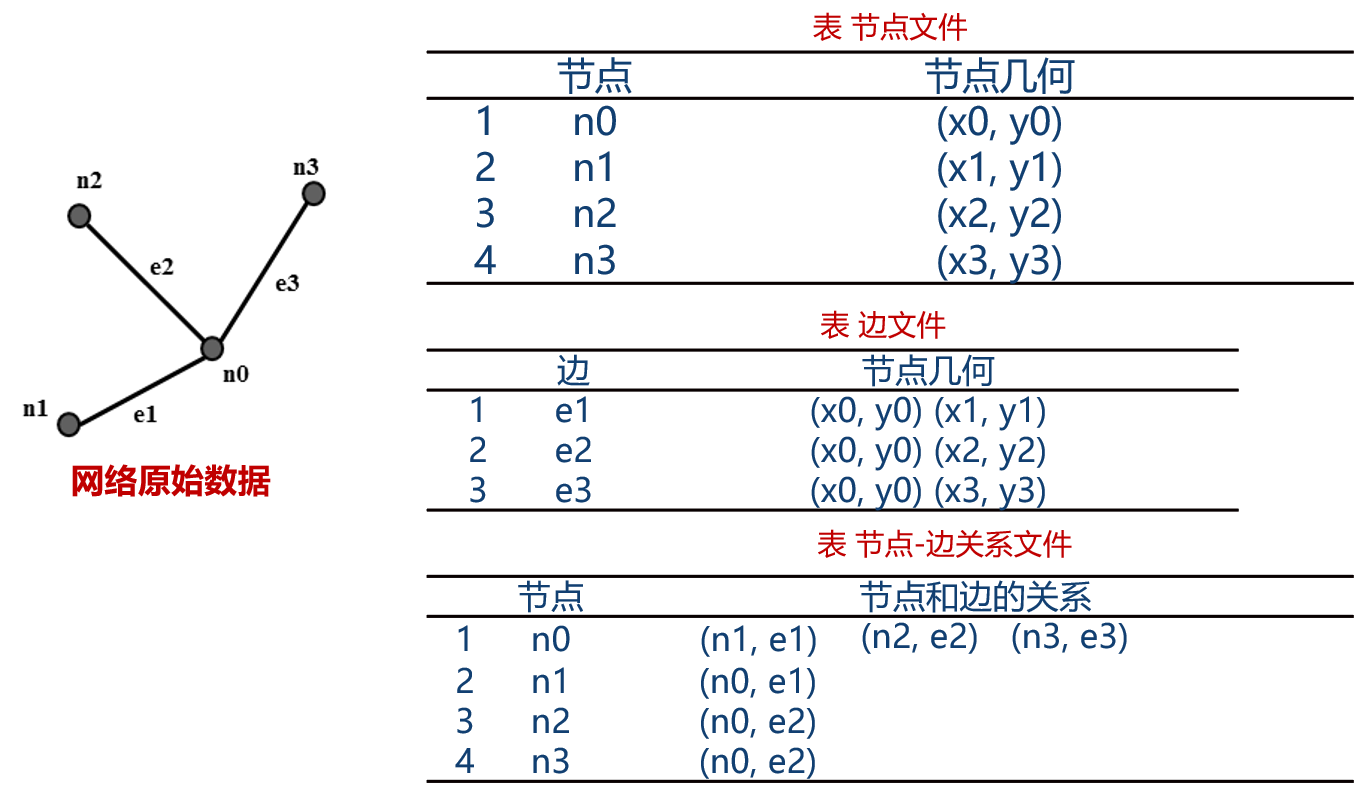
简单的几何网络结构用三个文件对其进行存储。一个是存储网络节点的文件，主要用于存储网络节点的几何特征，如节点的坐标信息。第二个是存储网络中边的几何信息的边文件，如果是有向网络，则需同时确定网络边的方向。尽管在几何网络中，通过节点和边的数据文件，就可以确定并绘制网络图，但无法确定网络中节点和边的拓扑关系，因此，还需要添加一个描述节点-边关系的数据文件，这在网络的连通性分析中是至关重要的。

这里仅列出了简单网络的几何数据结构，在实际应用中，网络建模要复杂得多。在较为复杂的网络中，可能需要考虑方向，还可能包含一级或多级的子节点和边，甚至还需要对转弯规则进行建模，如在道路建模中，某个道路交叉口只能左转弯，这都需要在网络结构中添加相应的规则。